2
[latexpage]
Introduction to this Lesson
All aircraft have operational limits in terms of the maximum and minimum airspeeds as well as altitudes at which they can fly level in steady, unaccelerated flight, e.g., the airspeed versus altitude boundary such as shown in the figure below. Notice that, by design, jet fighter aircraft can fly faster and higher over a wider range of flight conditions than other airplanes but remember that they also have a broader type of mission. In comparison, commercial jet airplanes are very much point designs in that they a designed primarily to cruise for long periods at a specific airspeed (or Mach number) and altitude. Turboprops are often used for short-haul flights, and while they fly at lower altitudes and airspeeds they are better suited for operating out of shorter runways.
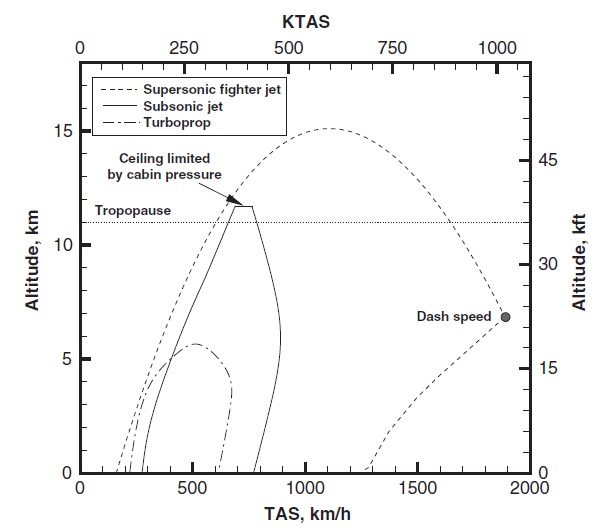
The area inside the boundaries that limit normal flight is called the airplane’s operational flight envelope. The limits of the envelope are defined and set based on aerodynamics (such as the highest achievable Mach number), the engine power (e.g., a turboprop or piston engine) or thrust (i.e., a turbojet or turbofan) that is available, the onset of maximum structural loads, or even something else such as the onset of flutter or buffeting. Limits could also be set by excessive aerodynamic heating for a supersonic aircraft. The flight corridor is often referred to as the speed range or band over which the airplane can fly at any given altitude without encountering any of the flight limits.
Objectives of this Lesson
- Understand the meaning of an airplane’s flight envelope and a flight corridor.
- Know about the various factors that may limit the operational flight envelope of an airplane, including stall.
- Have a general understanding of the phenomenon of wave drag and why it can also limit the flight envelope.
- Understand the principles associated with drag reduction using supercritical wing design and the area rule.
General Comments on the Flight Envelope
The size and shape of the flight envelope (or flight corridor) will depend on the type of airplane, i.e., whether it is propeller-driven or jet-powered, has an unpressurized or pressurized fuselage, and/or whether it is specifically designed for subsonic or supersonic flight. Naturally, the exact size and shape of the envelope for any given airplane also depends on the properties of the atmosphere, particularly the density and temperature of the air. Generally, the lowest attainable airspeed of an airplane (either jet-powered or propeller-driven) is dictated by the onset of wing stall, which determines the left side boundary on the flight envelope. This stalling airspeed will be a function of the airplane’s weight and altitude, as well as the wing flap settings and sometimes also if the undercarriage is up or down.
The right side of the boundary will be set by the highest attainable airspeed, which is usually limited by the power available (for propeller-driven airplanes) or thrust available (for jet engines) to overcome the drag of the airplane, the drag being a function of the shape of the airplane as well as its flight Mach number. The upper edge of the flight envelope is the maximum attainable altitude, which is referred to as the operational ceiling. The ceiling is the altitude above which an aircraft cannot climb, which is usually defined based on a threshold of a diminishing rate of climb of 100 ft/min. The attainable flight ceiling depends on the excess power available relative to the aircraft’s aerodynamic and other characteristics, including its weight. In some cases, however, such as on most commercial airplanes, the flight ceiling is limited by the onset of wave drag or transonic buffet, or by the airplane reaching some maximum structural loads associated with the pressurization of the fuselage (which is a trade with airframe weight), even though the airplane may have the excess power available to achieve higher flight altitudes.
Trimmed Lift Coefficient
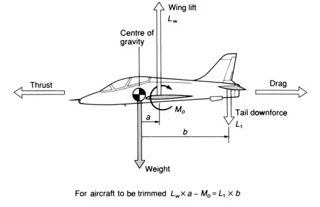
An airplane is said to be in steady level unaccelerated flight when the three forces (lift, drag and side force) and the three corresponding moments (pitching, rolling, and yawing) on the airplane are perfectly balanced, in which case the airplane is said to be in trim, as shown in the figure below. The balance of forces in steady trim is that vertical equilibrium requires that lift = weight and horizontal equilibrium requires that thrust = drag, i.e.,
\begin{equation}
L = W, \quad \quad T = D
\end{equation}
the side force is naturally assumed to be zero in trimmed flight. One other assumption here is that the thrust vector’s line of action is (primarily) in the flight direction. Of course, full flight trim also requires that the airplane have a moment balance in pitch, roll, and yaw about the center of gravity.
Remember that the wings generate the lift to overcome the weight and the engines provide the propulsive force to overcome the drag of the airplane, the generation of this thrust requiring a source of power and fuel. In terms of basic aerodynamics, for vertical equilibrium then
L = \frac{1}{2} \rho V_{\infty}^2 S C_L = W
\end{equation}
where $\rho$ is the density of the air in which the airplane is flying, $S$ is the reference wing area and $C_L$ is the total wing lift coefficient (the assumption here being that the wings generate all lift). Notice that $\rho = \rho_0 \sigma$ where $\sigma$ comes from the ISA model, i.e.,
\begin{equation}
L = W = \frac{1}{2} \rho_0 \sigma V_{\infty}^2 S C_L
\end{equation}
Rearranging this equation allows us to solve for the lift coefficient that needs to be produced on the wing for a given flight speed, i.e.,
\begin{equation}
C_L = \frac{2 W}{\rho_0 \sigma S V_{\infty}^2}
\label{CL eqn}
\end{equation}
or the flight speed that corresponds to a given lift coefficient, i.e.,
\begin{equation}
V_{\infty} = \sqrt{ \frac{2}{\rho_0 \sigma} \left( \frac{W}{S} \right) \frac{1}{C_L} }
\end{equation}
Recall that the ratio of airplane’s weight to its lifting wing area, $W/S$, is called the wing loading. Notice that the lift coefficient is proportional to weight (or to wing loading) but decreases with the square of the airspeed. The lift coefficient also increases with altitude for a given true airspeed and weight.
Stalling Airspeeds
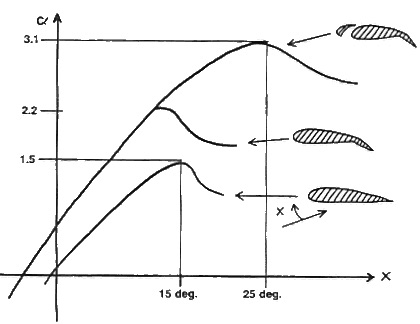
Although the value of $C_{L_{\rm max}}$ may not be exactly known by calculation, it can be determined indirectly from flight tests with the airplane from measurements of true airspeed and density altitude. After the $C_{L_{\rm max}}$ for the wing is determined, the stall speed in steady level flight can be solved for at any weight and density altitude. i.e.,
\begin{equation}
V_{\rm stall} = \sqrt{ \frac{2}{\rho_0 \sigma} \left( \frac{W}{S} \right) \frac{1}{C_{L_{\rm max}} } }
\label{stallspeed1}
\end{equation}
using the value of $\sigma$ from the ISA model, i.e., based on the prevailing pressure altitude and outside air temperature.
Notice that for a given $C_{L_{\rm max}}$, the stalling speed depends on the wing loading, i.e., all things being equal an airplane with a higher wing loading will stall at a higher airspeed. If a linear lift curve slope of the wing is assumed, say $C_{L_{\alpha}}$, then the angle of attack of the wing $\alpha$ (measured relative to the zero-lift angle) can be calculated using
\begin{equation}
\alpha = \frac{2 W}{\rho_0 \sigma S C_{L_{\alpha}} V_{\infty}^2}
\end{equation}
the maximum value of $\alpha$ typically being less than 15$^{\circ}$ at low Mach numbers and lower than that at higher Mach numbers. However, it is important to appreciate that a wing will stall at any airspeed if the angle of attack is high enough. For this reason, caution must be used when referring to stall speeds.
- Stall speed will increase with increasing weight of the airplane.
- Stall speed will increase with increasing density altitude, i.e., with a lowering of the air density.
- Stall speed will decrease with increasing values of wing $C_{L_{\rm max}}$, which, as previously discussed, can be achieved by the application of wing flaps and/or leading-edge slats.
- Stall speed will decrease with increasing wing area, an increase in wing area also being possible with the use of certain types of flaps, such as Fowler flaps.
Limiting Cruise Speeds
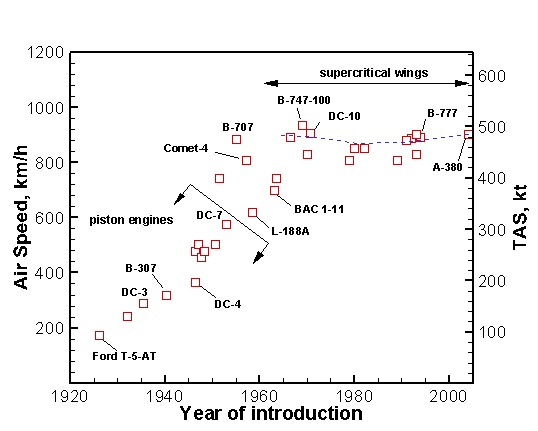
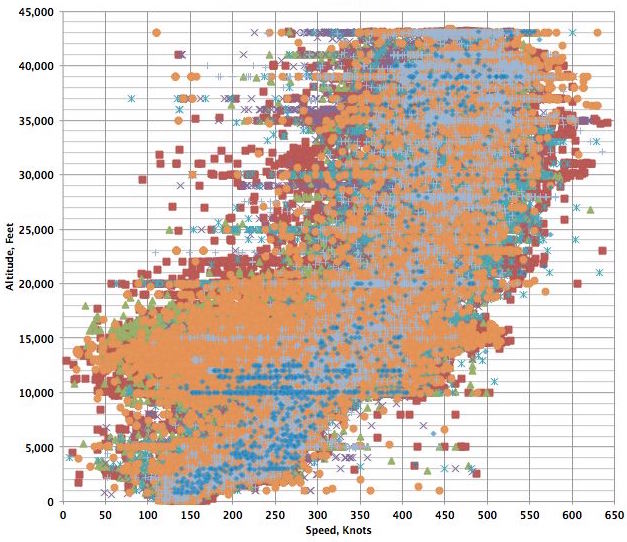
The figure below shows a historical trend as to how the cruise airspeeds for commercial transport airplanes have increased over the decades, which naturally is a direct consequence of the rapid advancements and maturation of aeronautical technology. Of course, the introduction of the jet engine was responsible for the more rapid growth in achievable cruise speeds seen after 1960. However, it can also be seen that since the early 1970s, the cruise airspeeds for commercial airplanes have all but plateaued, with corresponding achievable cruise flight Mach numbers in the range 0.8 to 0.85. There are a couple of exceptions to this trend with the British Concorde and the Russian Tu-144, but these airplanes were specifically designed for cruising at supersonic Mach numbers. While the use of supercritical wing designs has extended the flight envelope of airliners to higher transonic Mach numbers, the eventual onset of wave drag and buffeting still remains a physical barrier to higher flight conditions.
Supercritical Flows & Drag Rise
One reason is that cruise speeds for commercial airliners have reached a plateau is because of the buildup of high drag on a wing as transonic flow conditions are approached, the basic physics of what happens on the wing section being shown in the figure below. The drag buildup from the development of compressibility and shock waves takes much thrust and power to overcome, and there are other issues too about operating at higher flight Mach numbers such as buffeting, as has been discussed.
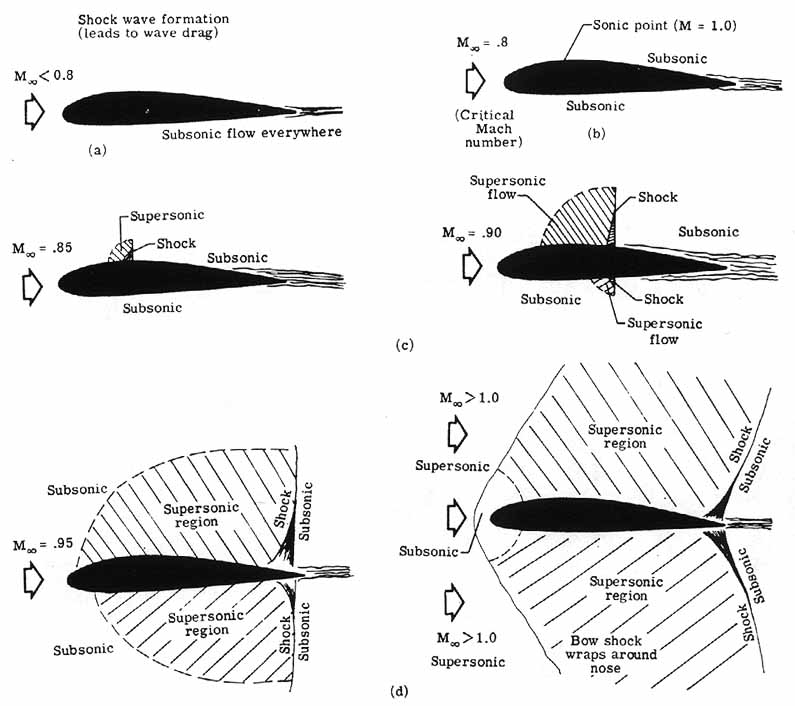
At some flight (free-stream) Mach number, the local flow at a point on the wing’s surface reaches sonic conditions, which is called the critical Mach number. As the free-stream Mach number increases further, a small pocket of supersonic flow develops on the section, resulting in a weak shock wave in the flow. As the Mach number further increases, the shock strengthens and moves aft over the section and a supersonic region is formed. An associated shock wave also develops on the lower surface. This is called the well-established transonic flow region, the shock waves resulting in an energy loss that manifests as form of drag called wave drag. Wave drag causes the total drag on the wing to increase rapidly, as shown in the figure below
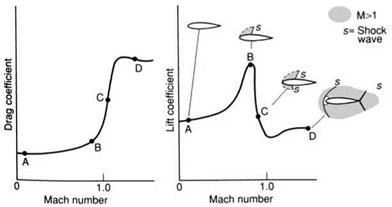
Because steep adverse pressure gradients also accompany the shock waves that develop during transonic conditions on the wing section, the boundary layer downstream of the shock becomes thicker and the profile drag increases. If the shock wave becomes sufficiently strong, flow separation may occur, leading to a buffeting aerodynamic phenomenon. Buffeting can result in high levels of vibration being transmitted to the airframe, and it is not a viably sustained flight condition. The onset of buffeting can also cause aeroelastic concerns, so this must be examined carefully through flight testing. The onset of buffeting is usually a limiting factor in the operational flight envelope of most aircraft (unless they are designed for supersonic flight) and is referred to as the buffet boundary.
If and when Mach number approaches unity, the shocks move all the way to the trailing edge of the section. Finally, when the Mach number becomes greater than one, a bow wave appears just ahead of the section, and the shocks at the trailing edge become oblique. For supersonic airplanes, these strong shock waves are responsible for the pressure changes that are heard on the ground that manifest as the impulsive “boom-boom” sound known as the sonic boom as the airplane passes overhead at supersonic speeds. The drag rise on the aircraft during the transition from transonic to supersonic flight usually requires excess thrust to be produced using an afterburner. Some aircraft may be subsequently able to cruise supersonically without the use of the afterburner, but it depends on the engine.
Reducing Compressibility Drag
The minimization of wave drag on the wings as the transonic flight regime is approached is obviously key to lowering drag and/or allowing the airplane to fly faster and opening up the flight envelope before significant drag rise is encountered. Lower drag means lower thrust and power is required for flight, so less fuel is expended and more flight range can be achieved.
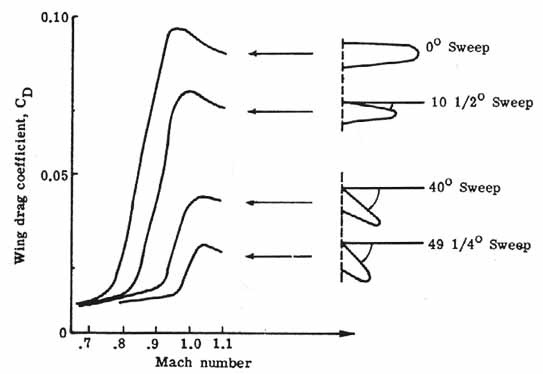
Wing sweep has a very profound effect on transonic and supersonic drag, as shown in the figure below. The use of swept-back wings reduces the strength of the shock waves and prevents the shocks from interfering with the flow over the wings and causing flow separation. However, although swept wings can help delay this drag rise from compressibility effects, other aerodynamic and aeroelastic problems are associated with swept wings, so aircraft designers ten to use as little wing sweep as possible, 20 to 30 degrees being used on may airliners.
A visualization of the flow about swept and unswept wings at a low supersonic speed is shown below, which was obtained using the schlieren method. Notice that with the use of sweepback the shockwaves do not interact directly with the wing, which keeps the drag low. With the unswept wings not only are the shock waves stronger but they interact strongly with the wing driving up drag.

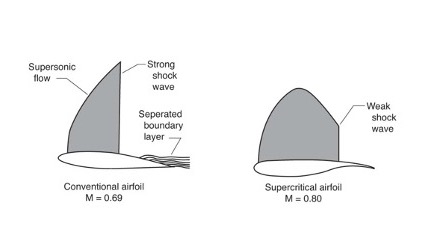
The figure below shows the difference in the shapes of a conventional airfoil and a supercritical airfoil. The basic principle used in transonic airfoil design is to control the flow’s expansion to supersonic speed and its subsequent recompression. Compared to a conventional wing section, a supercritical wing section is distinctive in that it is flatter along the top surface with significant camber at its trailing edge. variations of supercritical airfoil sections are used on all commercial jet airliners.
The challenges in reaching higher transonic cruise speeds have led to the design of a special shape of swept wing called a supercritical wing, as shown in the photograph below. The supercritical wing evolved from the careful tailoring of the airfoil section(s) with the overall wing design to delay the formation and/or reduce the strength of the shock waves over the wing so reducing wave drag. In the early 1970s, NASA modified an airplane to test a supercritical wing in place of the conventional wing to reduce the effects of shock waves and wave drag, with great success, and aircraft designers have never looked back.

Area Rule
Other ways of reducing wave drag expanding the flight envelope of the airplane to higher cruise speeds include the use of the area rule, which was developed by Richard Whitcomb. To reduce the number and intensity of shock waves over an airplane as it approaches transonic and then supersonic flight, the basic design principle behind the area rule is that the airplane’s overall cross-sectional shape should change smoothly with no significant discontinuities.
The principle was proven to work in wind tunnel testing and then applied retroactively to various airplanes, with successful results after flight testing. Early airplanes that were modified to validate the area rule had distinctive if not odd looking “waisted” fuselage shapes at the wing root, as shown in the figure below, which were often dubbed as “flying coke bottles.” Nevertheless, the notable reductions in drag proved the viability of the area rule concept.
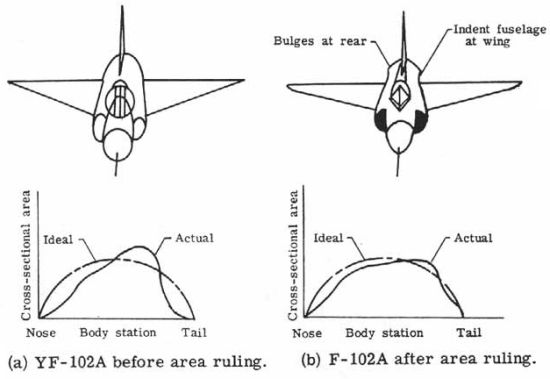
Later airplanes were designed with the area rule in mind but were aesthetically more pleasing because of the blending of the wing root area and the careful positioning of engines, the use of large trailing edge anti-shock wing pods or “canoe” fairings, and other subtle changes to the shape of the airplane to prevent large changes in effective cross-sectional area. For many commercial airplanes, the wing-mounted “pod” engines are placed relatively far forward of the wings to control the change in cross-sectional area of the airplane as the wing is approached.

A careful examination of the most commercial airliners will show some careful contouring of the fuselage and wing root to help minimize wave drag according to the principles established by the area rule. For the same reason, later versions of the Boeing 747 were also modified with a longer upper deck and a shallower transition at its end to keep area changes as progressive as possible. Most airplanes capable of transonic or supersonic airspeeds incorporate design features that can be traced back to the fundamental principles underlying Whitcomb’s area rule.
Flight Ceilings
The flight ceiling for an airplane is defined based on a demonstrated rate of climb. The absolute ceiling is defined when the achievable rate of climb diminishes to zero, whereas the service ceiling is defined such that the rate of climb reduces below 100 ft/min. The airplane’s normal performance ceiling is defined as when the rate of climb reduces below 200 ft/min. The ceiling is reached when the excess power available over and above that for level flight at the same airspeed and weight becomes diminishingly small.
The ceiling for most commercial transport airplanes is limited by cabin pressurization requirements rather than attainable engine thrust and power, which set a structural stress limit on the fuselage; for most airplanes, the cabin pressure is maintained at an altitude equivalent to about 6–8,000 ft to allow for good passenger comfort. Nevertheless, some passengers may still exhibit some of the symptoms of hypoxia (oxygen deprivation) during long flights, which contribute to the malady known as jet lag. The most modern commercial transport airplanes such as the Boeing 787 maintain the cabin pressure at the equivalent of 6,000 ft (i.e., at a higher pressure differential), which improves passenger comfort and reduces the effects of jet lag.
Representative Flight Envelopes
The general idea of a flight envelope has already been introduced, although now having learned about the specifics of airspeed and Mach number, stalling, transonic drag rise, and the thrust/power required for flight, the characteristics of the flight envelope of an airplane and why it has inherent boundaries can be understood. Stalling speeds always define the low speed end of the envelope, and the onset of transonic drag rise and buffet will define the high speed end of the envelope. The ceiling is defined by the allowable differential pressurization, which is a structural limit not an aerodynamic one as previously explained.
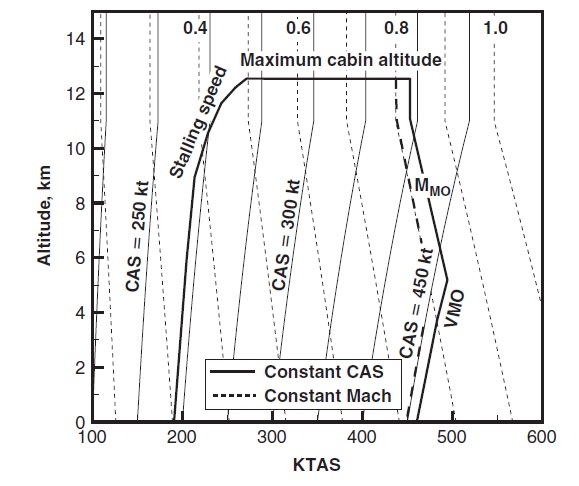
A representative flight envelope for a commercial subsonic transport (jet) airplane is shown in the figure below, with an actual measured flight envelope with test points identified shown in the figure below. In this case, the graphs are defined in terms of the airspeed and the flight Mach number, the significance of the Mach number already being discussed. At lower airspeeds, the envelope is bounded by the stalling speeds, which is in the “clean” configuration. The stall region of the flight envelope needs little further elaboration other than it is a complex aerodynamic region involving flight at low airspeeds and high angles of attack, which also depends on how the airplane is configured, e.g., flaps up or down, landing gear up or down, etc. The stall boundary is always defined carefully during flight testing, and usually requires many tests to establish good confidence that the stall boundary and the handling qualities and other characteristics of the airplane at stall have been explored for all combinations of flight (e.g., weights and altitudes).
At higher airspeeds, the limits of flight are dictated by the maximum operating Mach number, which is called $M_{\rm mo}$, with the corresponding airspeed being called the maximum operating airspeed $V_{\rm mo}$ or VMO. In operational service, the airplane will cruise at an airspeed that is somewhat lower than this recommended airspeed (which will appear in the airplane’s operating manual and procedures).
While fundamental engineering issues are key here, there are non-engineering factors that may limit the actual usable flight envelope. For example, there are issues centered around economic requirements, manufacturability, passenger ergonomics and safety, airfield requirements, and environmental and noise regulations. For example, an airline always wants to maximize its profit because the higher the profit per unit weight of payload carried, the higher the profit. In this respect, the empty weight of the airplane is critical. The benefit is that not only is the fuel burn lower (i.e., lower costs for a given payload), but the revenue can also be increased by carrying more payload. This is one of the reasons why the use of lightweight composite materials has become so critically important in modern aircraft design.This not because composites are necessarily lighter per se but because they can be better tailored to give a better strength to weight ratio.
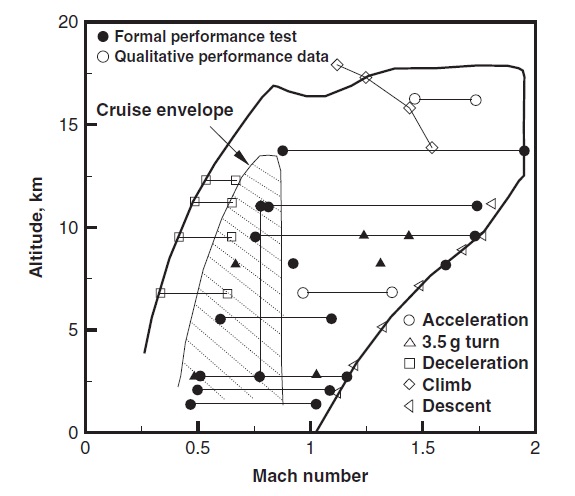
The figure below shows the flight envelope of high-performance jet airplanes that can reach supersonic flight speeds, at least at higher altitudes. In this case, the envelope has again been established with the aid of flight test, which has included various types of maneuvers, including accelerations, decelerations, climbs, and descents. Notice the relatively broad flight envelope for this airplane in terms of attainable altitudes and airspeeds (Mach numbers). However, such high-performance airplanes tend to expose the limits of aeronautical technology, which tie closely to the limitations imposed by aerodynamics and the strength of the airframe and the engines.
Other Limiting Factors on the Flight Envelope
The engines themselves may suffer various problems that may limit the airplane’s flight boundary, including surge/stall issues and intake buzz. Intake “buzz” is usually associated with supersonic airplanes, which have inlets designed to reduce the flow speeds to subsonic conditions before the flow enters the engine’s compressor stage. The buzz phenomenon, if it occurs, involves the interaction between the surface boundary layer flows and the shock waves, which can result in an unsteady flow behavior at the intake to the engine.
Engine surges can occur on all types of jet engines when stall manifests in the compressor stage. However, the onset is usually precipitated by a high operating angle of the airplane’s attack, especially when at lower airspeeds. The phenomenon results in a sudden back pressure through the engine, resulting in unstable engine operation. In some cases, the combustion process is interrupted to the degree that raw fuel ends up burning in the tailpipe, often resulting in a spectacular discharge of smoke and flames.
While serious in that surges cause an immediate loss of thrust, they are usually quickly self-correcting when the conditions that promoted the problem are removed, i.e., by the pilot reducing the angle of attack of the wing and/or increasing airspeed by pushing forward on the control stick. Nevertheless, engine surge conditions have been known to manifest more often during the critical takeoff and climb phases of flight, which always poses a safety of flight issue. Usually, an engine that suffers from surging must be closely inspected for damage before further flight.

Wing flutter is an aeroelastic phenomenon, a coupling between the aerodynamic loads and the elastic deformation of the structure. Wings and tail surfaces are prone to flutter at higher airspeeds and Mach numbers, although other parts of the airframe such are the engine nacelles and tail surfaces may also be susceptible to such problems. Even on a wing, the onset of flutter is not necessarily catastrophic and can manifest as a benign (but often alarming) limit-cycle torsional and/or bending oscillations.
Generally, however, the avoidance of flutter is a key design requirement. The structural dynamics and potential flutter characteristics of the aircraft’s structure are carefully examined using computer models, the objective being to identify the natural frequencies and modes of deformation; as shown below. The parameters that may affect the onset of flutter on a wing include the geometry of the wing (its span, aspect ratio, thickness, sweep angle, etc.) as well as its structural stiffness, total weight and weight distribution, positions and weights of the engines, moments of inertia about the bending and torsional axes, etc.

Even with a good understanding of the flexible airframe, however, flutter developments can still occur. Flutter usually leads to large structural deformations and even to structural failure. Because the onset of flutter conditions on an airplane can be potentially catastrophic, wings, in particular, are designed carefully to avoid the problem and then verified by flight testing to ensure that flutter will never occur if the airplane is flown properly within its normal validated flight envelope.
Some Final Comments.
All aircraft will have an operational flight envelope that is defined in terms of the airspeeds and altitudes where the aircraft can be flown safely with it aerodynamics and performance limits. In this regard, not all aircraft are created equally. The advent of the supercritical airfoil design and redevelopment of the supercritical wing allowed for a significant increase in the flight envelope of commercial airliners and other aircraft that cruise in transonic flow. The characteristic flat top surfaces of supercritical airfoil is apparent on all modern jetliners. The use of the area rule has allowed not only reductions in wave drag but have allowed aircraft to cruise more efficiently at a higher transonic Mach number.
For Further Thought and/or Discussion
- Think about the nature of the flight envelope for a small, general aviation airplane powered by a reciprocating engine and propeller.
- What factors will limit the lowest and highest achievable airspeeds?
- What operational flight envelope would a typical helicopter have compared to an airplane? A tiltrotor?
- Study photos you can find of the Airbus A380. Can you identify any design features that tie to the use of the “area rule” in its design.
- What type of flight envelope would a supersonic transport (SST) aircraft have? What factors will limit the highest achievable flight Mach number?
Other Useful Online Resources
To learn more about the supercritical airfoil check out this article by NASA.

