Soil Physics

Morty Morterson; carl123

Soil Physics

Mass-Volume relationships

Mass-volume relationships can be used to define many soil physical properties, including porosity, soil bulk density, and the relative proportions of water and air occupying pore space in a soil.

The total mass of soil (Fig. 3) is comprised of the mass of solid (M_s), the mass of liquid (M_l) and the mass of gas (M_g). Note however, that the mass of the gas is negligible, and can be assumed equal to zero.

(1) $\begin{equation*}M_{t} = M_{s} + M_{l} + M_{g}\end{equation*}$

Similarly, the total volume of soil is $V_{t}$ is comprised of the volume of solid ( $V_{s}$ ), the volume of liquid ( $V_{l}$ ), and the volume of gas ( $V_{g}$ ). As the volumes of liquid and gas make up the volume of voids or pores,

(2) $\begin{equation*}V_{f} = V_{l} + V_{g}\end{equation*}$

and the total volume of soil,

(3) $\begin{equation*}V_{t} = V_{s} + V_{l} + V_{g}\end{equation*}$

In the SI system, the unit of mass is kilogram (kg) and the unit of volume is cubic meters (m³). Similarly, in the centimeter-gram-second (CGS) system the unit of mass is gram (g) and the unit of volume is cubic centimeter (cm³).

Densities ( $\rho$ ):

The relationship between mass and volume for any material in a phase is related to its density. The relationship can be written as

(4) $\begin{equation*}Mass = {Volume} \times {Density}\end{equation*}$

(5) $\begin{equation*}Density = \frac{Mass}{Volume}\end{equation*}$

The unit of density is mass unit over volume unit or kg m^-3 (SI Unit) or g cm^-3 (CGS unit).

Particle density ( $\rho_{p}$ ): The density of solid (or soil) particles can be calculated as

(6) $\begin{equation*}\rho_{p} = \frac{M_{s}}{V_{s}} = \frac{\text{Mass of solid}}{\text{Volume of solid}}\end{equation*}$

The unit of ρp is kg m^-3 (SI Unit) or g cm^-3 (CGS unit). In calculating ρp, it is difficult to measure the volume of solids in a soil system; unlike the total volume of soil which includes the volume of air and water. Based on the most common minerals found in soil (i.e., quartz and feldspar), the ρp of a mineral soil ranges between 2,600 kg m^-3 and 2,700 kg m^-3 (or between 2.6 g cm^-3 and 2.7 g cm^-3). Typically, the average value, 2,650 kg m^-3 (or 2.65 g cm^-3) is used for calculating other soil physical properties. Similarly, ρp of organic materials is about 1,300 kg m^-3 (or 1.30 g cm^-3).

Liquid or water density ( $\rho_{l}$ ): The density of liquid (or water) can be calculated as

(7) $\begin{equation*}\rho_{l} = \frac{M_{s}}{V_{l}} = \frac{\text{Mass of liquid}}{\text{Volume of liquid}}\end{equation*}$

The unit of ρl is kg m^-3 (SI Unit) or g cm^-3 (CGS unit). For most calculations, the density of water is assumed 1,000 kg m^-3 (or 1.0 g cm^-3).

Dry bulk density ( $\rho_{b}$ ): The dry bulk density can be calculated as

(8) $\begin{equation*}\rho_{b} = \frac{M_{s}}{V_{t}} = \frac{\text{Mass of solid}}{\text{Volume of total soil}}\end{equation*}$

The unit of $\rho_{b}$ is kg m^-3 (SI Unit) or g cm^-3 (CGS unit). Note that ρb accounts for only the mass of solid. As the name implies, $\rho_{b}$ includes the mass of dry soil. The $\rho_{b}$ of most mineral soils varies between 1,000 to 1,800 kg m^-3. However, this can be impacted by natural processes (e.g., shrink/swell, aggregation, freeze/thaw) and management practices such as tillage, logging, or grazing. Thus, bulk density is often considered a dynamic property at or near the soil surface, though it is reasonably constant lower in the soil profile. Unlike mineral soils, organic soils (soils with organic matter >30% by weight) generally have ρb ranging between 800 and 1,000 kg m^-3 with values as low as 500 kg m^-3 in soils with very high levels of undecomposed organic matter (e.g., peat soils).

Water content ( $\theta$ )

It is the amount of water (or liquid) present in a soil system. It can be calculated on a mass basis (known as gravimetric water content, $\theta_{w}$ ) or volume basis (known as volumetric water content, $\theta_{v}$ ) as the ratio of $M_{w}/{M_{t}$ or $V_{w}/{V_{t}$ , respectively. Being a ratio, it is dimensionless. However, the unit of numerator and denominator are often maintained to indicate the type of water content or the calculation procedure. For example, the unit of $\theta_{w}$ is kg kg^-1 or g g^-1 and the unit of $\theta_{v}$ is m³ m^-3 or cm³ cm^-3; thus, the unit indicates the type of water content and the calculation procedure. For example, a value of 0.22 kg kg^-1 of soil indicates the amount of gravimetric water content or $\theta_{w}$ of 0.22. Without an indication of units or specification about the type of water content (gravimetric or volumetric), the value of 0.22 alone can be confusing and misleading. This ratio can further be multiplied by 100 to express the water content in percentage, i.e., 22% water content on a mass or gravimetric basis in this example.

Mass-based or gravimetric water content ( $\theta_{w}$ ): The mass-based water content also known as gravimetric water content can be calculated as,

(9) $\begin{equation*}\theta_{w} = \frac{M_{l}}{M_{s}} = \frac{M_{t} - M_{s}}{M_{s}} = \frac{\text{Mass of liquid (water)}}{\text{Mass of solid}}\end{equation*}$

This is expressed as either dimensionless with specification of gravimetric water content or kg kg^-1 or g g^-1.

Volume-based or volumetric water content ( $\theta_{v}$ ): The volume-based water content also known as volumetric water content can be calculated as,

(10) $\begin{equation*}\theta_{v} = \frac{V_{l}}{V_{t}} = \frac{\text{Volume of liquid (water)}}{\text{Volume of soil}}\end{equation*}$

This is expressed as either dimensionless with specification of volumetric water content or m³ m^-3 or cm³ cm^-3. However, measurement of the volume of liquid in a soil system is very difficult. Thus, often the volumetric water content is estimated from a simple relationship between gravimetric water content and bulk density (see Eq. 14).

Porosity

Porosity is the amount of pore space (or the space occupied by liquid and gas phases) in a soil system. It is an index for the relative volume of pores in the soil. The total volume of pores including that occupied by liquid and gas phases is known as total porosity ( $f$ ). The pores occupied by gas (or air) is known as air-filled (or aeration) porosity and the pores occupied by liquid (or water) is known as water filled porosity. It is the ratio of two volumes (volume of pores to volume of soils) and the units are m³ m^-3 (SI Unit) or cm³ cm^-3 (CGS unit). This ratio can be converted to percentage by multiplying with 100.

Total porosity ( $f$ ): indicates the total pores or voids in a soil system and is calculated as

(11) $\begin{equation*}f = \frac{V_{f}}{V_{t}} = \frac{V_{l} + V_{g}}{V_{t}} = \frac{\text{Volume of voids (liquid + gas)}}{\text{Volume of soil}} = \frac{V_{t} - V_{s}}{V_{t}}\end{equation*}$

The unit of $f$ is m³ m^-3 (SI Unit) or cm³ cm^-3 (CGS unit). The ratio can also be converted into percentage by multiplying with 100. In general, for a mineral soil, $f$ varies between 0.3 and 0.6 m³ m^-3. For sandy soils or soils with an abundance of large particle sizes, $f$ tends to be smaller, while for clay dominated soils or soils with finer particles, $f$ tends to be larger. Remember, large size particles can create larger pores than the smaller sized particles. However, the total number of pores and pore volume are higher in soils with finer particles. Note that total porosity does not provide any information about the pore-size distribution. Surface soils tend to have high porosity and the volume of pores generally decrease with depth in the soil profile as the soil bulk density tends to increase.

Water-filled porosity ( $f_{w}$ ): the pores filled with water in a soil system and is calculated as,

(12) $\begin{equation*}f_{w} = \frac{V_{l}}{V_{t}} = \frac{\text{Volume of liquid (water)}}{\text{Volume of soil}} = \theta_{v}\end{equation*}$

The unit of $f_{w}$ is m³ m^-3 (SI Unit) or cm³ cm^-3 (CGS unit).

Air-filled porosity or aeration porosity ( $f_{a}$ ): the pores filled with gas (air) in a soil system and is calculated as,

(13) $\begin{equation*}f_{a} = \frac{V_{g}}{V_{t}} = \frac{\text{Volume of gas (air)}}{\text{Volume of soil}}\end{equation*}$

The unit of $f_{a}$ is m³ m^-3 (SI Unit) or cm³ cm^-3 (CGS unit). Air-filled porosity is the proportion of the bulk soil occupied by air at any point in time. It is related to the total porosity, and volumetric water content, as both air and water share the same pore volume. Air-filled porosity can then be determined by subtracting the volumetric water content (cm³ of water per cm³ of soil) from the total porosity of the soil. As soil water content varies in time and with soil depth, so does air-filled porosity. Its value will be minimal following significant rainfall or irrigation events. Typically, values should be higher than 0.10 to 0.15 cm³ cm^-3 at field capacity, following drainage.

Relationships among soil physical parameters

While many physical quantities can be calculated from the mass-volume relationships of the three phases, measurement of mass and volumes of different phases are sometimes difficult. Alternatively, easy to measure parameters may be used to estimate parameters that are more difficult to measure. Some useful formulas are provided below.

Relationship between volumetric water content ( $\theta_{v}$ ), gravimetric water content ( $\theta_{w}$ ) and bulk density ( $\rho{b}$ ) can be written as,

(14) $\begin{equation*}\theta_{v} = \theta_{w}\rho_{b}\end{equation*}$

Relationship between total porosity ( $f$ ), bulk density ( $\rho_{b}$ ), and particle density ( $\rho_{p}$ ) can be written as,

(15) $\begin{equation*}f = 1 - \frac{\rho_{b}}{\rho_{p}}\end{equation*}$

Relationship between total porosity ( $f$ ), air-filled porosity ( $f_{a}$ ), and volumetric water content ( $\thetA_{v}$ ) can be written as,

(16) $\begin{equation*}f_{a} = f - {\theta_{v}\end{equation*}$

SOIL WATER MOVEMENT

Saturated and unsaturated soil water flow

Water flows in soil from locations of high total potential to locations of low total potential. The magnitude of vertical soil water flow under saturated and unsaturated soil conditions are described by two very similar equations. Flow of water in saturated soils (i.e., when all soil pores are water-filled) is described by Darcy’s Law:

(17) $\begin{equation*}q_{w} = -K_{s}\frac{\Delta H}{\Delta z}\end{equation*}$

where $q_{w}$ is the soil water flux density with units of $\frac{m^3 H_2 O}{m^2 soil\cdot s}$ ; $K_{s}$ is called the saturated hydraulic conductivity having units of $\frac{m^3 H_2 O}{m^2 soil\cdot s}$ per unit of hydraulic gradient; and $\frac{\Delta H}{\Delta z}$ is the hydraulic gradient (i.e., the change in sum of pressure and gravitational potentials over some depth interval, $\Delta z$ ); is dimensionless when $h_{p}$ is expressed in m H₂O.

The negative sign in Darcy’s law is used to specify flow direction. Upward flow (i.e., flow in the increasing z direction, is positive and downward flow, in the decreasing z direction, is negative). Downward flows are associated with positive gradients ( $\frac{\Delta H}{\Delta z}$ > 0), meaning the total potential decreases with decreasing depth.

Edgar Buckingham acknowledged that soils were often unsaturated (i.e., only a fraction of the pores were water-filled), and under these conditions, the hydraulic gradient depends on changes in matric potential within the soil, and that the hydraulic conductivity under unsaturated conditions changes with soil wetness. The result is the Buckingham-Darcy Flux Law:

(18) $\begin{equation*}q_{w} = -K(\theta)\frac{\Delta H}{\Delta z}\end{equation*}$

where, $K(\theta)$ is the hydraulic conductivity as a function of water content, simply referred to as the unsaturated hydraulic conductivity, and $\frac{\Delta H}{\Delta z}$ is the hydraulic gradient (i.e., the change in sum of pressure and gravitational potentials over some depth interval, $\Delta z$ )

Hydraulic Conductivity

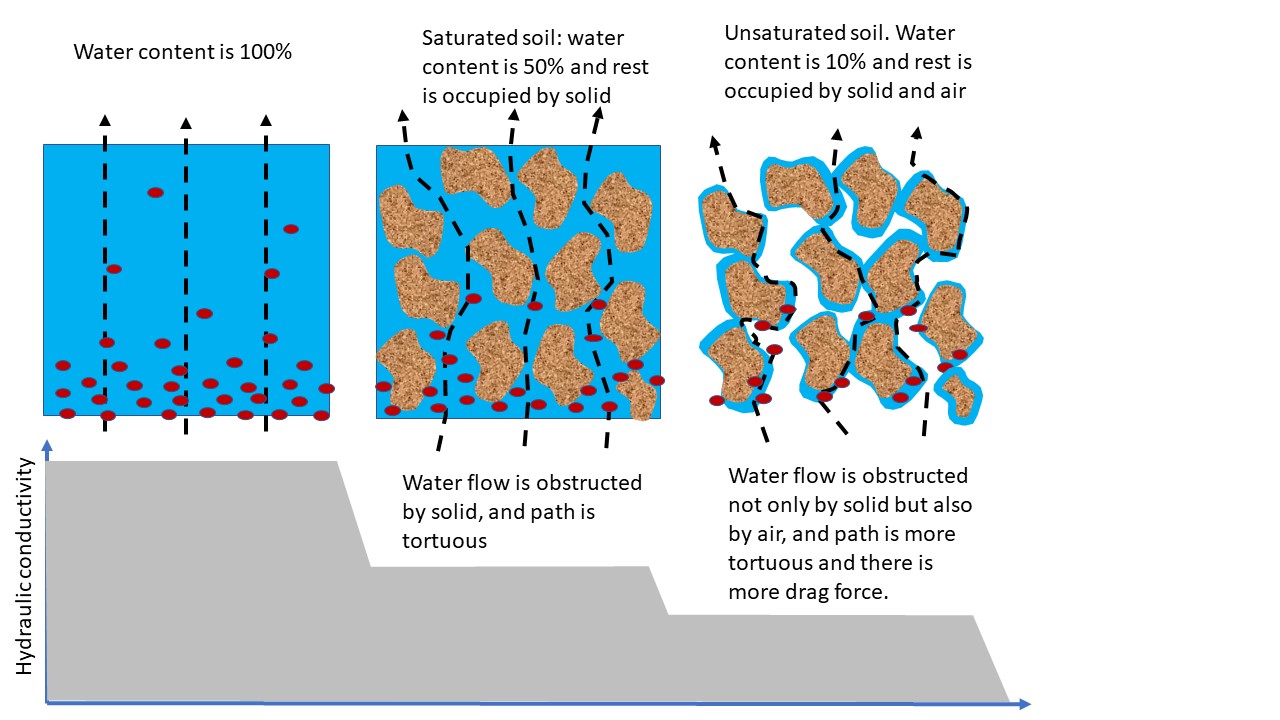
The hydraulic conductivity ( $K$ ) is a soil hydraulic property that represents the soil’s ability to facilitate water flow. Each soil has a unique hydraulic conductivity that is related to the pore-size distribution of the soil. Fig. 4.7 shows K as a function of matric potential for soils with three different textures. When saturated, soils with large, continuous pores will have a much greater hydraulic conductivity compared to soils with small, discontinuous pores. As soil water content decreases, the hydraulic conductivity decreases because: (1) the total volume of water-filled pores decreases; and (2) the size of water-filled pores decreases (Fig. 8). Therefore, soil hydraulic conductivity is a function of the volumetric water content.

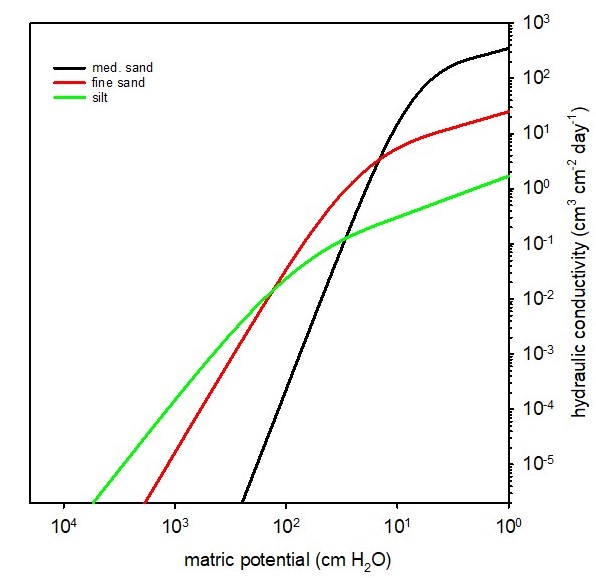
At saturation, the hydraulic conductivity of each soil reaches the maximum value ( $K_{s}$ ), the saturated hydraulic conductivity, but decreases exponentially as the soil becomes drier (y-axis for hydraulic conductivity is on a logarithmic scale). The high Ks of the loamy sand relative to the loam and silty clay loam soils is a reflection of the larger pores associated with coarse-textured soils.

**Figure 4.8.** Reduction in flow pathways with decreasing soil water content. © Bing Si. CC BY.

Hydrological processes and the soil water balance

The soil water balance

The soil water budget represents the balance between inputs and outputs from a given soil unit (Eqn. 20). Soil water storage (ΔS) is one component in a water balance. It refers to the change in water storage volume within a given soil unit over a specified time period, and is usually expressed in equivalent height of water per unit time (e.g., mm day-1).

(19) $\begin{equation*}P + I - ET + Q_i - Q_o - \Delta S - DP = 0\end{equation*}$

where, $P$ = precipitation; $I$ = irrigation; $ET$ = evapotranspiration; $DP$ = drainage and deep percolation; $Q_i$ = other inflow (e.g., capillary rise, and water table fluctuations); and $Q_o$ = other outflow, (e.g., runoff and lateral flow).

Water balance measurements (e.g., using measuring devices called lysimeters) are time and resource consuming, and thus estimates may be made from basic site measurements of soil water content and potential, soil properties and weather data over a given time interval.

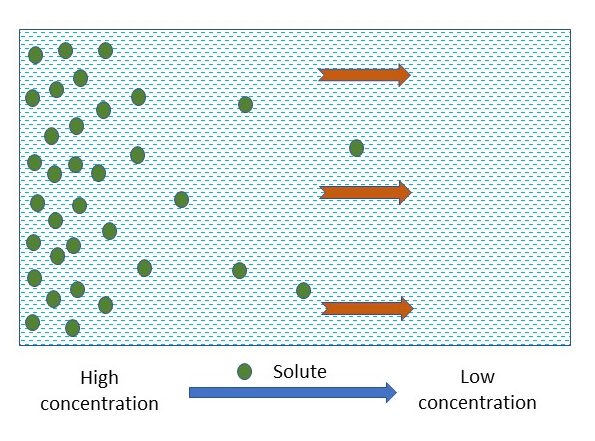
Molecules in a liquid have an internal kinetic energy. As a result, a molecule in a static liquid is in constant motion. The direction in which an individual molecule moves is constantly changing due to its collision with neighboring molecules, known as Brownian motion. While individually, each molecule moves randomly, without a preferred direction, collectively, more ions or molecules tend to move from areas of higher concentration to area of lower concentration (Fig. 4.10). In fact, the larger the concentration difference over a certain distance, the faster the spread. To quantitatively measure the rate of the spread we define the flux, as the mass of solute moved perpendicularly across a unit area per unit time (kg m^-2 s^-1), following Fick’s law of diffusion.

(20) $\begin{equation*}q_s = -D_s\frac{\Delta C}{\Delta x}\end{equation*}$

where: $q_s$ is the chemical flux (kg m^-2 s^-1); $\Delta C$ is the concentration difference between two locations ( $\Delta C = C_2 - C_1$ ) separated by distance $\Delta x$ ( $\Delta x = x_2 - x_1$ ); and $D_s$ is and a proportionality constant called the diffusion coefficient (m² s^-1).

**Figure 4.10.** Solute (e.g., Cl^–, NO₃^–) flows from high concentration to low concentration in water. © Bing Si. CC BY.

Mass flow

Solute transport by diffusion occurs within soil solution, but the water as a whole remains stationary. However, when water is under a pressure gradient in the soil, it will move from high potential to low potential, and any constituents in solution or suspension will move with the water. This movement of water and solutes together due to a pressure gradient, is called mass flow. The amount of a solute transported per unit area of soil by mass flow is given by the solute flux ( $q_s$ , kg m^-2 s^-1), which is the product of the water flux and the solute concentration in the solution:

(21) $\begin{equation*}q_s = q_wC\end{equation*}$

where, $q_w$ is the water flux (m s^-1) and $C$ is the solute concentration in water (kg m^-3).

Worked Example #1 – bulk density & gravimetric water content

Zineb, a student at the University of British Columbia, collected a soil core from the UBC Farm during summer. The sample is weighed, oven dried at 105ºC for 24 hours (or constant weight) and re-weighed.

[table “10” not found /]

Calculate the bulk density and gravimetric water content of this soil sample (show formulas used and units).

Step 1: Calculation of bulk density

We know $\rho_b = \dfrac{M_s}{V_t}$

where $M_s$ = mass of solids and $V_t$ = total soil volume

Thus, $\rho_b = \dfrac{M_s}{V_t} = \dfrac{386.1\,g}{330\,cm^3} = 1.17\,g\,cm^{-3}$

Step 2: Calculation of gravimetric water content

We know that $\theta_w = \dfrac{M_l}{M_s} = \dfrac{M_{fresh} - M_{oven\;dry}}{M_s}$

where

$M_{fresh} = (fresh\,mass\,of\,soil + core) - mass\,of\,core = 499.4\,g -56.0\,g = 443.4\;g$

Thus, $\theta_w = \dfrac{443.4\,g - 386.1\,g}{386.1\,g} = \dfrac{57.3\,g}{386.1\,g} = 0.15\,g\,g^{-1}$

Worked Example #2 – gravimetric & volumetric water content

A soil sample collected from the Chaudière-Appalaches region of Quebec has a gravimetric water content (θ_w) of 0.19 g g^-1 and a bulk density (ρ_b) of 1.26 g cm-3. What is the volumetric water content (θ_v) of this sample in cm³ cm^-3? Show all formulas, units and full calculation.

We know that $\theta_v = \dfrac{V_l}{V_t}$ and $\theta_w = \dfrac{M_l}{M_s} = \dfrac{M_t - M_s}{M_s}$

Now, $\rho_l = \dfrac{M_l}{V_l}$ or $V_l = \dfrac{M_l}{\rho_l}$ and $\rho_b = \dfrac{M_s}{V_t}$ or $V_t = \dfrac{M_s}{\rho_b}$

Thus, $\theta_v = \dfrac{V_l}{V_t} = \dfrac{\frac{M_l}{\rho_l}}{\frac{M_s}{\rho_b}} = \dfrac{M_l \cdot \rho_b}{M_s \cdot \rho_l} = \theta_w\dfrac{\rho_b}{\rho_l}$

Now, if we consider the density of liquid (or water in this case) = 1 g cm^-3 (in CGS unit), then we can simply write $\theta_v = \theta_w\rho_b$

For the soil sample from the Yukon (showing full units):

$\theta_v = \theta_w\rho_b = 0.19 g g^{-1} \times \dfrac{1.26 \frac{g}{cm^3}}{1 \frac{g}{cm^3}} = 0.24 \frac{cm^3}{cm^3}$

Worked Example #3 – bulk density & porosity

A loam soil in Southern Alberta has a porosity of 48%. What is bulk density of this soil in kg m^-3? Show all formulas you use and the full calculation including units.

Assuming a particle density of $2.65\frac{kg}{m^3}$ and given a porosity of 48% or $0.48\frac{cm^3}{cm^3}$ , the bulk density is $1,378\frac{kg}{m^3}$

This calculation is done by rearranging and solving the following equation:

Porosity $= 1 - \frac{\rho_b}{\rho_s}$ where $\rho_b$ is soil bulk density and $\rho_s$ is soil particle density.

Therefore: $\rho_b = 2.65 \frac{g}{cm^3} - (2.65 \frac{g}{cm^3} \times 0.48) = 1.378 \frac{g}{cm^3} = 1,378 \frac{kg}{m^3}$

Worked Example #4 – Soil water movement

Miles, who teaches introductory soil science at the University of Alberta, took measurements of soil water tension (T) at 3 depths, before and after a large rain event. Unfortunately, some of the measurements were lost.

A) Fill in the two tables below using the following information:

the soil solution contains no salts and the soil is well vented to atmosphere
all three points (or depths) of observation are above the water table (or free water surface)
the reference point is set at the soil surface

[hint: remember that $T = - \text{matric potential}$ ( $h_m$ )]

Table I

[table “12” not found /]

Table II

[table “13” not found /]

B) Which table belongs to the measurements taken before the rain event, and which after? Briefly explain.

Solution:

determinie $h_g$ : since the reference elevation is at the surface, and the units are m of water, $h_g$ is the same as the depth, i.e., increasingly negative as we move deeper in the soil profile and farther below the reference elevation
recall that the matric potential ( $h_m$ ) = $-\; T$
as the soil solution contains no salts, the osmotic potential $h_o = 0$
as the soil is well vented, and the soil profile is above the water table, $h_p = 0$
recall $h_t = \Sigma(h_g + h_m + h_o + h_p)$
recall that soil water moves from high to low potential, thus you can determine the direction of flow

Table I

[table “14” not found /]

Table II

[table “15” not found /]

B) Table I shows the data after the rain, since the direction of water flow in the surface part of the profile (i.e., from point A to B) is downward. Downward water movement implies that water is entering the soil.

Table II shows data before the rain. In Table II, the water is moving upward, from point B to point A, which is an indication that that part of soil profile is drier (probably due to combination of evapotranspiration and water uptake in that part of soil by roots and soil organisms).

Worked Example #5 – Solute transport / nitrate leaching in soil

Fernanda, a student at the University of Saskatchewan conducted a column experiment. The diameter of the soil column was 20 cm. She applied a constant rate of NO₃^– solution on the top of soil column. When the amount of solution collected from the bottom of the column reached steady state (i.e., the flux was constant with time), 30 mL of solution was collected in 30 minutes.

A) Calculate the soil water flux

The water flux is $q_w = \dfrac{V}{At}$ where $A$ is the cross-sectional area of the column ( $\pi r^2$ ); thus,

$q_w = \dfrac{30\,cm^3}{3.14\cdot (10\,cm)^2\cdot 30\,min} = 0.00318\,cm\,min^{-1}$

Fernanda also took a sample of the collected solution and measured the NO₃^–concentration using ion Chromatography (IC). The measured concentration of NO₃^– was 10 μg L^-1.

B) Calculate the NO₃^– flux

The NO₃^– flux can be calculated using Equation # 22:

$q_s = q_wC = 0.00318\,cm\,min^{-1}\,\cdot\,10\,\mu g\,L^{-1}\cdot\,0.001\,L\,cm^{-3}$

$q_s = 3.18\cdot 10^{-5}\,\mu g \,cm^{-2}\,min^{-1}$

Alternatively, we can calculate the flux based on the definition of chemical flux:

$mass\,of\,chemicals = V \cdot C = 30 \,cm^3 \cdot 10 \,\mu g\,L^{-1} \cdot 0.001 \,L \,cm^{-3} = 0.3 \,\mu g$

thus,

$q_s = \dfrac{m}{At} = \dfrac{0.3\, \mu g}{3.14\cdot (10\,cm)^2\cdot 30\,min} = 3.18\cdot 10^{-5}\,\mu g\,cm^{-2}\,min^{-1}$

License

Icon for the Public Domain license

This work (Math Test by Morty Morterson and carl123) is free of known copyright restrictions.