"

Exponents in Algebra

If you are like most Canadians, your employer pays you biweekly. Assume you earn 12.00 per hour. How do you calculate your pay cheque every pay period? Your earnings are calculated in as follows:

12.00 × (hours worked during the biweekly pay period)

The quantity “hours worked during the biweekly pay period” is the unknown variable. Recall that the word variable simply represents a quantity that can vary in value. Notice that the expression above appears lengthy when you write out the explanation for the variable. Algebra uses symbols to make such expressions more convenient to manipulate. To shorten the expression, making it easier to read, we can assign a letter or a group of letters to represent the variable. In this case, you might choose h to represent “hours worked during the biweekly pay period.” This rewrites the above expression as follows:

12.00 \times h or simply  12h

Unfortunately, the word algebra makes many people worry. But remember that algebra is just a set of tools that can help in solving a numerical problem. It is used to demonstrate how the pieces of a puzzle fit together to arrive at a solution.

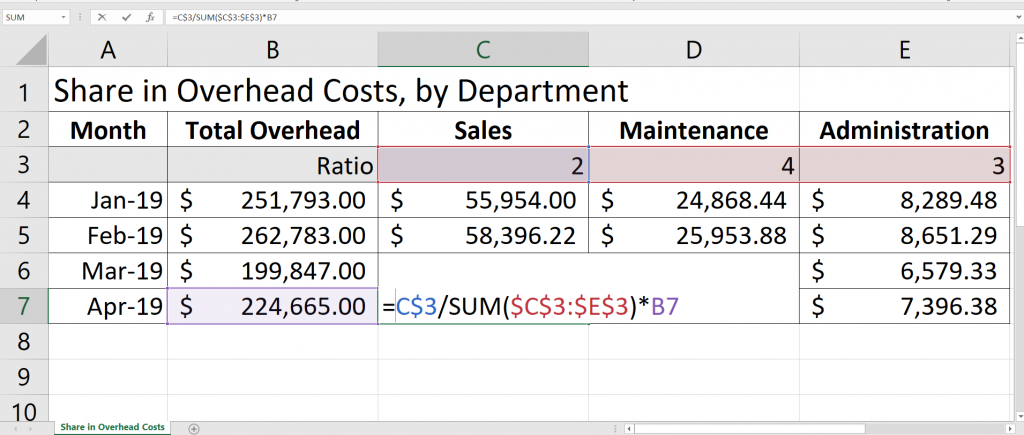
For example, you have used your algebraic skills if you have ever programmed a formula into Microsoft Excel. You told Excel there was a relationship between cells in your spreadsheet. Perhaps your calculation required cell C3 to be divided by the sum of cells C3, D3 and E3, and then multiplied by cell B7. This is an algebraic expression. Excel then took your algebraic expression and calculated the solution by automatically substituting in the appropriate values from the referenced cells (your variables). See the example below:

C7=C3/SUM(C3:E3)*B7 <img class="aligncenter wp-image-1060 size-large" src="https://ecampusontario.pressbooks.pub/app/uploads/sites/1786/2021/08/1-1_Excel_formula_example-1024x435.png" alt="Screenshot of an Excel worksheet demonstrating use of formulas" width="1024" height="435" /> Algebra involves integrating many interrelated concepts. In this textbook we will discuss the concepts that are important to business mathematics. Your understanding of algebra will become more complete as more concepts are covered over the course of this book. This section reviews the language of algebra, including exponent rules, basic operation rules, and substitution. In Section 1.2 you will put these concepts to work in solving one linear equation for one unknown variable along with two linear equations with two unknown variables. Finally, in Section 1.3 you will explore the concepts of logarithms and natural logarithms. <h2>The Language of Algebra</h2> Understanding the rules of algebra requires familiarity with four key definitions. <h3>Algebraic Expressions</h3> A mathematical algebraic expression indicates the relationship between the specific values represented by numbers or variables and the mathematical operations that must be conducted on these values. For example, iflatex hrepresents the number of hours worked and the hourly wage islatex $12, the expressionlatex 12hcalculates the total amount of dollars earned forlatex hhours worked. Note that, even though by convention we don't write a multiplication symbol in this expression,latex 12hrepresentslatex 12\cdot h. Specifically,latex 12must be multiplied by the value oflatex h. Note also that an expression does not include an equal sign, or "latex =". An expression only tells you what to do and requires that you substitute a value in for the unknown variable(s) to solve. There is no one definable solution to the expression - an expression can represent many different values, potentially infinitely many. The value of the expression will change as the value of the variables in the expression change. An algebraic expression <strong>is not the same thing as </strong>an algebraic equation, however an algebraic equation is built from algebraic expressions. <h3>Algebraic Equations</h3> An <strong>algebraic equation</strong> is a statement that says two algebraic expressions are equal. This equation can often, but not always, be solved to find a solution for the unknown variables. Examine the following illustration to see how algebraic expressions and algebraic equations are interrelated. Consider two algebraic expressions:latex 6x+3yandlatex 4x+3Each of these expressions represents a value that can be calculated if we were given values forlatex xandlatex y. By writinglatex 6x+3y=4x+3we are imposing a condition on these two expressions, stating that they must produce equal values. This in turn imposes a condition on the values oflatex xandlatex y; we can potentially no longer substitute any value forlatex xandlatex ybecause we may end up with a statement that is not true. <div class="textbox Concept Check"> <h4><strong>Concept Check</strong></h4> <span style="font-size: 1rem;">Can you determine whether a particular value or a set of values is a solution to a given equation? Try it out:</span> MathMatize: <a href="https://mathmatize.com/learn/tip/e15ea196-deb5-4c18-bccc-bc397ec58dac" target="_blank" rel="noopener">Verifying solutions to equations</a> </div> <h3>Terms</h3> In any algebraic expression, terms are the components that are separated by addition and subtraction. In looking at the example above, the expressionlatex 6x + 3yis composed of two terms. These terms arelatex 6xandlatex 3y. A <strong>nomial</strong> refers to how many terms appear in an algebraic expression. If an algebraic expression contains only one term, likelatex 12h, it is called a <strong>monomial</strong> (mono = one). If the expression contains two terms or more, such aslatex 6x + 3y, it is called a <strong>polynomial</strong> (poly = many). <h3>Factors</h3> Terms may consist of one or more <strong>factors</strong> that are separated by multiplication or division signs. For example,latex 6xconsists of two factors. These factors arelatex 6andlatex x; they are joined by multiplication to createlatex 6x. <ul> <li>If the factor is numerical, it is called the <strong>numerical coefficient</strong>.</li> <li>If the factor is a variable or a product of two or more variables, it is called the<strong> literal coefficient</strong>.</li> </ul> In practice, the term most commonly used is simply <strong>coefficient</strong> and it represents the numerical coefficient in the term. Here is an example, also shown in the figure below: Suppose we have an equation of the formlatex \frac{7x}{3}+4xy^2=x^3-2yEach side of the equation is composed of different terms, which are in turn composed of different factors, and the two sides are connected by the equal sign, making this a statement of equality, i.e., an equation. The left side is a sum of two terms:latex \frac{7x}{3}andlatex 4xy^2. The termlatex \frac{7x}{3}can be rewritten aslatex \frac{7}{3}xand is therefore composed of two factors:latex \frac{7}{3}andlatex x. In this form of the term,latex \frac{7}{3}is the coefficient oflatex x. On the right side we have the difference of two terms:latex x^3andlatex 2y. The termlatex x^3can be thought of as a single factor, it can be thought of as composed of the three factorslatex x,latex xandlatex xor as composed oflatex 1\cdot x^3. The latter is very useful when algebraic rules require you to consider the (numerical) coefficient of the term. If no numerical coefficient is stated, it is implied to be 1. The second term on the right side of the equation islatex -2yand it is composed of the coefficientlatex -2and the variablelatex y. Indeed, this can get very confusing. But with practice you can get very familiar with the language of algebra and thus be able to use it to solve complex problems. <div class="textbox Concept Check"> <h4><strong>Concept Check</strong></h4> <span style="font-size: 1rem;">Check your understanding of the terms <em>equivalent expressions, coefficients </em>and <em>factors</em> through this series of multiple choice exercises:</span> MathMatize: <a href="https://mathmatize.com/c/272?task=edab38c9-d38b-4991-83c5-a1418c02318e">E<span style="font-size: 1rem;">quivalent expressions, coefficients and factors</span></a> </div> <h3>Exponents</h3> Exponents are widely used in business mathematics and are integral to mathematics of finance. For example, when applying compounding interest rates to any investment or loan, you must use exponents. The basic meaning of <strong>exponent</strong> is a mathematical shorthand notation that indicates how many times a quantity is multiplied by itself. However, this can be expanded to a more general concept involving exponents. Whenlatex n is a natural number (latex 1, 2, 3, \ldots ) andlatex bis an arbitrary number, we use the symbolslatex b^n

    to represent <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-a72d8e1e732b9feb0f7df07c8af44865_l3.svg" height="37" width="124" class="ql-img-displayed-equation " alt="\[ b^n = \underbrace{b\cdot b\cdot b \cdots b}_{n\text{ times}}\]" title="Rendered by QuickLaTeX.com"/> We say that <strong><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-6fdf9c070cfe038293a327fefe10d62b_l3.svg" class="ql-img-inline-formula " alt="b" title="Rendered by QuickLaTeX.com" height="12" width="8" style="vertical-align: 0px;"/> is raised to the exponent <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-7116d97420433739a1191f012b8657f9_l3.svg" class="ql-img-inline-formula " alt="n" title="Rendered by QuickLaTeX.com" height="8" width="11" style="vertical-align: 0px;"/></strong>. The format of an exponent is illustrated below: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-4eced363c0a7e78703a25b2d8c395123_l3.svg" height="21" width="158" class="ql-img-displayed-equation " alt="\[ \text{base}^{\text{exponent}}=\text{power}\]" title="Rendered by QuickLaTeX.com"/> where <ul> <li><strong>base</strong> is the quantity that is multiplied by itself</li> <li><strong>exponent</strong> is the number that indicates how many times the base is to be multiplied by itself</li> <li><strong>power</strong> is the result of performing the multiplication</li> </ul> Assume you have

latex 2^3 = 8. The exponent of 3 says to take the base of 2 multiplied by itself three times, orlatex 2 × 2 × 2. The power is 8. The proper way to state this expression is "8 is the power of 2 to the exponent of 3." <h4>Rules and definitions in operations with exponents</h4> Many rules apply to the simplification of powers, as shown in the table below. <table style="border-collapse: collapse; width: 100%; height: 142px;" border="0"> <tbody> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;"><strong>Operation</strong></td> <td style="width: 33.3333%; height: 14px;"><strong>Rule</strong></td> <td style="width: 33.3333%; height: 14px;"><strong>Explanation</strong></td> </tr> <tr style="height: 44px;"> <td style="width: 33.3333%; height: 44px;">1. Multiplying powers with the same base</td> <td style="width: 33.3333%; height: 44px;">latex y^ay^b = y^{a+b}</td> <td style="width: 33.3333%; height: 44px;">When multiplying powers with the same base, copy the original base and raise it to the sum of the original exponents.</td> </tr> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;">2. Dividing powers with the same base</td> <td style="width: 33.3333%; height: 14px;">latex \dfrac{y^a}{y^b} = y^{a-b}</td> <td style="width: 33.3333%; height: 14px;">When dividing powers with the same base, copy the original base and raise it to the difference of the original exponents.</td> </tr> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;">3. Power of a power</td> <td style="width: 33.3333%; height: 14px;">latex (x^a)^b = x^{ab}</td> <td style="width: 33.3333%; height: 14px;">When a power is raised to an exponent, copy the base of the original power and raise it to the product of the original exponents.</td> </tr> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;">4. Power of a product</td> <td style="width: 33.3333%; height: 14px;">latex (xy)^a=x^ay^a</td> <td style="width: 33.3333%; height: 14px;">When raising a product to an exponent, multiply the original factors, each raised to the original exponent.</td> </tr> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;">5. Power of a quotient</td> <td style="width: 33.3333%; height: 14px;">latex \left(\dfrac{x}{y}\right)^a=\dfrac{x^a}{y^a}</td> <td style="width: 33.3333%; height: 14px;">When raising a quotient to an exponent, divide the original numerator and denominator, each raised to the original exponent.</td> </tr> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;">6. Zero exponents</td> <td style="width: 33.3333%; height: 14px;">latex y^0 = 1</td> <td style="width: 33.3333%; height: 14px;">By definition, any nonzero base raised to exponent 0 is equal to 1. (Note that <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-32114d07d485ec326b93bfbc1d95c04f_l3.svg" class="ql-img-inline-formula " alt="0^0" title="Rendered by QuickLaTeX.com" height="15" width="16" style="vertical-align: 0px;"/> is undefined.)</td> </tr> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;">7. Negative exponents</td> <td style="width: 33.3333%; height: 14px;">latex y^{−a} = \frac{1}{y^a}</td> <td style="width: 33.3333%; height: 14px;">By definition, a base raised to a negative exponent is 1 divided by the original power but with the positive exponent.</td> </tr> <tr style="height: 14px;"> <td style="width: 33.3333%; height: 14px;">8. Fractional exponents</td> <td style="width: 33.3333%; height: 14px;">latex y^{\frac{a}{b} }= \sqrt[b]{y^a}</td> <td style="width: 33.3333%; height: 14px;">A fractional exponent is a different way of writing a root. When a power has an exponent that is a fraction, the denominator of the original exponent represents the root of the base raised to the numerator of the original exponent.</td> </tr> </tbody> </table> <h4>Important Notes</h4> Recall that mathematicians do not normally write the numberlatex 1when it is multiplied by another factor because it doesn't change the result. The same applies to exponents. If the exponent is alatex 1, it is generally not written because any number multiplied by itself only once is the same number. For example, the numberlatex 2could be written aslatex 2^1, but the power is stilllatex 2. Or take the case oflatex (yz)^a. This could be written aslatex (y^1z^1)^a, which when simplified becomeslatex (y^{1a}z^{1a})orlatex y^az^a. Thus, even if you don't see an exponent written, you know that the value of the exponent islatex 1

    . <div class="textbox textbox--examples"><header class="textbox__header"> Example: Exponents in Algebra </header> <div class="textbox__content"> Simplify the following expressions: <table class="no-lines" style="border-collapse: collapse; width: 100%;" border="0"> <tbody> <tr> <td style="width: 16.6667%;">a. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-05510062efeaf299b9cf30ed0cacba0c_l3.svg" class="ql-img-inline-formula " alt="h^3h^6" title="Rendered by QuickLaTeX.com" height="15" width="35" style="vertical-align: 0px;"/></td> <td style="width: 16.6667%;">b. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-f1db3754750605e567c98f4087380513_l3.svg" class="ql-img-inline-formula " alt="\dfrac{h^4}{h^8}" title="Rendered by QuickLaTeX.com" height="39" width="18" style="vertical-align: -12px;"/></td> <td style="width: 16.6667%;">c. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-30e8f1aec213438209c9b7ca95390797_l3.svg" class="ql-img-inline-formula " alt="\left[\dfrac{hk^5m^3}{n^4}\right]^3" title="Rendered by QuickLaTeX.com" height="47" width="77" style="vertical-align: -16px;"/></td> <td style="width: 16.6667%;">d. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-93737314e84ba875a6ad93fb34af3c70_l3.svg" class="ql-img-inline-formula " alt="1.49268^0" title="Rendered by QuickLaTeX.com" height="15" width="65" style="vertical-align: 0px;"/></td> <td style="width: 16.6667%;">e. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-f67b23975ff0bfd6de17c12da85ffa17_l3.svg" class="ql-img-inline-formula " alt="\dfrac{x^2y^4}{xy^-2}" title="Rendered by QuickLaTeX.com" height="43" width="40" style="vertical-align: -16px;"/></td> <td style="width: 16.6667%;">f. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-f1af05e18074f8685718fed9ce503858_l3.svg" class="ql-img-inline-formula " alt="6^{3/5}" title="Rendered by QuickLaTeX.com" height="16" width="30" style="vertical-align: 0px;"/></td> </tr> </tbody> </table> <strong>Answers:</strong> a. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-c596109ed73a78db337a30e4b9dc2841_l3.svg" height="17" width="135" class="ql-img-displayed-equation " alt="\[h^3h^6=h^{3+6}=h^9\]" title="Rendered by QuickLaTeX.com"/> (multiplication of powers with the same base) b. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-59dbba5f41c9292458e5bdf3b254264f_l3.svg" height="39" width="175" class="ql-img-displayed-equation " alt="\[\dfrac{h^4}{h^8}=h^{4-8}=h^{-4}=\dfrac{1}{h^4} \]" title="Rendered by QuickLaTeX.com"/> (division of powers with the same base; negative exponent definition) c. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-023cedce51606c4fd20906588b085323_l3.svg" height="49" width="400" class="ql-img-displayed-equation " alt="\[ \left[\dfrac{hk^5m^3}{n^4}\right]^3=\dfrac{\left(hk^5m^3\right)^3}{(n^4)^3}=\dfrac{h^3(k^5)^3(m^3)^3}{n^{12}}=\dfrac{h^3k^{15}m^9}{n^{12}} \]" title="Rendered by QuickLaTeX.com"/> (power of a quotient, power of a product; power of a power) d. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-7944a51835dc9fb45a3eecb9c528234d_l3.svg" height="17" width="96" class="ql-img-displayed-equation " alt="\[ 1.49268^0=1\]" title="Rendered by QuickLaTeX.com"/> (definition of zero exponent) e. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-a04a2615d82ebcb7a448a93d228420f4_l3.svg" height="43" width="295" class="ql-img-displayed-equation " alt="\[ \dfrac{x^2y^4}{xy^{-2}}=\dfrac{x^2}{x}\cdot \dfrac{y^4}{y^{-2}}=x^{2-1}y^{4-(-2)}=xy^6 \]" title="Rendered by QuickLaTeX.com"/> (factoring of fractions, dividing powers with the same base) f. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-4e688b0e392ed0701cf6c5674efc3239_l3.svg" height="18" width="86" class="ql-img-displayed-equation " alt="\[6^{3/5}=\sqrt[5]{6^3}\]" title="Rendered by QuickLaTeX.com"/> (definition of fractional exponents) </div> <div></div> <div></div> </div> <div class="textbox Concept Check"> <h4><strong>Concept Check</strong></h4> Check through these exercises if you can state the laws of the exponents and apply them. MathMatize: <a href="https://mathmatize.com/c/272?task=63d08903-d72e-4d08-9ac5-8b839502c82c">Laws of Exponents</a> </div> <h3>Addition and Subtraction of Algebraic Expressions</h3> Simplifying unnecessarily long or complex algebraic expressions is always preferable to increase understanding and reduce the chances of error. For example, assume you are a production manager looking to order bolts for a product that you make. Your company makes three products, all in equal quantity. Product A requires seven bolts, Product B requires four bolts, and Product C requires fourteen bolts. If <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-fbf91c0f04ab67fc3d062a80c3736e96_l3.svg" class="ql-img-inline-formula " alt="q" title="Rendered by QuickLaTeX.com" height="12" width="8" style="vertical-align: -4px;"/> represents the quantity of products required, you need to order

latex 7q + 4q + 14qbolts. This expression requires four calculations to solve every time (each term needs to be multiplied bylatex qand you then need to add everything together). With the algebra rules that follow, you can simplify this expression tolatex 25q. This requires only one calculation to solve. So what are the rules in general? <div class="textbox shaded"> <h4>Simplifying sum and/or difference of like terms</h4> In math, monomials with the same variable components (i.e., same literal coefficients) are called <strong>like terms</strong>. When it comes to addition and subtraction of monomials, only like terms may be added or subtracted. Monomials with like terms are added and/or subtracted by adding or subtracting their coefficients, as indicated by the addition or subtraction operation. </div> From the previous example, you requirelatex 7q + 4q + 14q

    bolts. Notice that there are three monomial terms, each of which has the same variable component, <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-fbf91c0f04ab67fc3d062a80c3736e96_l3.svg" class="ql-img-inline-formula " alt="q" title="Rendered by QuickLaTeX.com" height="12" width="8" style="vertical-align: -4px;"/>. Therefore, you can perform the required addition by adding the three coefficients: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-af5a5b87df8495ef5ee48e2afe962196_l3.svg" height="19" width="279" class="ql-img-displayed-equation " alt="\[ 7q + 4q + 14q=(7+4+14)q=25q \]" title="Rendered by QuickLaTeX.com"/> <h4>Things To Watch Out For</h4> A common mistake in addition and subtraction is combining terms that do not have the same variable component. You need to remember that the variable components must be identical. For example,

latex 7qandlatex 4qhave the identical variable component, which islatex q. However,latex 7qandlatex 4q^2have different variable components,latex qandlatex q^2, and therefore cannot be added or subtracted (but they can be multiplied or divided, using exponent laws). <h4>Paths To Success</h4> Remember that if you come across a variable component with no coefficient in front of it, that coefficient is assumed to be alatex 1. For example,latex xhas no written coefficient, but it is the same aslatex 1x. Another example would belatex \frac{x}{4}, which is the same aslatex \frac{{1x}}{4}orlatex \frac{1}{4}x. On a similar note, mathematicians also don't write out variable components that have variables with exponent of zero. For example,latex 7x^0is justlatex 7(1)orlatex 7. Thus, the variable component is always there; however, it the variable has an exponent of zero. Remembering this will help you later when you multiply and divide in algebra. <h4>Give It Some Thought</h4> Examine the following algebraic expressions and indicate how many terms can be combined through addition and subtraction. No calculations are necessary. Simplify as much as possible. <ol> <li>latex \frac{3}{2}x + 4{x^2} – 10x – 2y + \frac{x}{3}</li> <li>latex 23{g^2} – \frac{{17{g^2}}}{5} + {g^4} + {g^2} – \frac{2}{3}{g^2} – 0.15g + {g^3}</li> </ol> <em>Answers:</em> <ol> <li>Three like terms (all of thelatex x), <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-b19129ab57b5ced00834fedd3ceb8f7b_l3.svg" class="ql-img-inline-formula " alt="-\frac{49}{6}x+4x^2-2y" title="Rendered by QuickLaTeX.com" height="22" width="129" style="vertical-align: -6px;"/></li> <li>Four terms (all of thelatex g^2

    ), <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-bb548191879a88a28bf9f3ff26bac498_l3.svg" class="ql-img-inline-formula " alt="-0.15g+\frac{299}{15}g^2+g^3+g^4" title="Rendered by QuickLaTeX.com" height="22" width="193" style="vertical-align: -6px;"/></li> </ol> <div class="textbox textbox--examples"><header class="textbox__header"> Example: Addition and Subtraction in Algebra </header> <div class="textbox__content"> Simplify the following algebraic expressions. a. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-5b11376afba7e1a93715905d30ae85cd_l3.svg" class="ql-img-inline-formula " alt="9x+3y-\frac{7}{2}x+4y" title="Rendered by QuickLaTeX.com" height="22" width="141" style="vertical-align: -6px;"/> b. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-01b1a9048fae5a99d578673ec9c161a5_l3.svg" class="ql-img-inline-formula " alt="P\left(1+0.11\cdot \frac{121}{365}\right)+\frac{15P}{1+0.11\cdot\frac{36}{365}}" title="Rendered by QuickLaTeX.com" height="29" width="224" style="vertical-align: -13px;"/> c. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-4fdce34e06c2caf56e7fc13adc56c1c4_l3.svg" class="ql-img-inline-formula " alt="x\left(1+\frac{0.1}{4}\right)^3+\frac{x}{\left(1+\frac{0.1}{4}\right)^4}-\frac{3x}{\left(1+\frac{0.1}{4}\right)^2}" title="Rendered by QuickLaTeX.com" height="36" width="254" style="vertical-align: -17px;"/> <strong>Answers:</strong> a. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-685558812388adcce2c88c0bef29beea_l3.svg" class="ql-img-inline-formula " alt="9x+3y-\frac{7}{2}x+4y=\left(9-\frac{7}{2}\right)x+(3+4)y=\frac{11}{2}x+7y" title="Rendered by QuickLaTeX.com" height="23" width="411" style="vertical-align: -7px;"/> b. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-f352502230d99798524f3d9102a9f982_l3.svg" height="208" width="3252" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-15c1554edbc3a3e0572795f37438375c_l3.svg" height="208" width="498" class="ql-img-displayed-equation " alt="\begin{align*} P\left(1+0.11\cdot \frac{121}{365}\right)+\frac{15P}{1+0.11\cdot\frac{36}{365}}&=P(1+\frac{13.31}{365})+\frac{15}{1+\frac{3.96}{365}}P\\ &=\frac{378.31}{365}P+\frac{15}{\frac{368.96}{365}}P\\ &=\frac{378.31}{365}P+15\cdot\frac{365}{368.96}P\\ &=\left(\frac{378.31}{365}+15\cdot\frac{365}{368.96}\right)P\\ &\approx 15.875473P \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> c. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-2f5b66614ec257eba631876f4de4919c_l3.svg" height="185" width="3200" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-8a5a769d683e981ce10d69ed0ffa16dc_l3.svg" height="185" width="441" class="ql-img-displayed-equation " alt="\begin{align*} x\left(1+\frac{0.1}{4}\right)^3+&\frac{x}{\left(1+\frac{0.1}{4}\right)^4}-\frac{3x}{\left(1+\frac{0.1}{4}\right)^2}\\ &=\left(\frac{4.1}{4}\right)^3x+\frac{1}{\left(\frac{4.1}{4}\right)^4}x-\frac{3}{\left(\frac{4.1}{4}\right)^2}x\\ &=\left(\frac{4.1}{4}\right)^3x+\left(\frac{4.1}{4}\right)^{-4}x-3\left(\frac{4.1}{4}\right)^{-2}x\\ &\approx -0.872602x \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> </div> </div> <h4>Paths To Success</h4> The order in which you write the terms of an algebraic expression does not matter as long as the order of operations is clear, but there are some general conventions with following general principles: <ul> <li>coefficient, then variable component</li> <li>decreasing order of exponents</li> <li>alphabetical order of variables if multiple variables</li> </ul> Here are examples of some expressions written by following these principles; see if you can recognize each principle at play: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-d139a88a3113772885617d317120be16_l3.svg" height="15" width="64" class="ql-img-displayed-equation " alt="\[5.2x+4\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-8fb7c6f2dcb5c4b3db61eb8a44f21f33_l3.svg" height="19" width="142" class="ql-img-displayed-equation " alt="\[-1.9x^5+3x^2-7x\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-e9feee72092ca159b0e716b6740882d8_l3.svg" height="22" width="143" class="ql-img-displayed-equation " alt="\[w(w^2-1)(w-5)^4\]" title="Rendered by QuickLaTeX.com"/> <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-207887c83a774e750b2993de9d1ca6b0_l3.svg" height="21" width="71" class="ql-img-displayed-equation " alt="\[2x^2y^5z^{-6}\]" title="Rendered by QuickLaTeX.com"/> <h3>Multiplication of algebraic expressions</h3> When <strong>multiplying two monomials</strong>, we must multiply <em>like</em> with <em>like</em>, then simplify. Specifically, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-8d26092f3301b6cbef79bfdfde05eab8_l3.svg" height="16" width="250" class="ql-img-displayed-equation " alt="\[ ax^n\cdot bx^m=ab\cdot x^nx^m=abx^{n+m}\]" title="Rendered by QuickLaTeX.com"/> In other words, multiply the product of the coefficients with the product of the powers of the variable(s). For example, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-a978c8ba1807adb5063fc208fe77b3b2_l3.svg" height="22" width="195" class="ql-img-displayed-equation " alt="\[ 1.2x^{5}\cdot (-3x^{-2})=-3.6x^{3}\]" title="Rendered by QuickLaTeX.com"/> When <strong>multiplying a monomial with a binomial</strong>, we must multiply the monomial with each term in the binomial and add the resulting terms together. Specifically, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-f45b894a545bf45650561a7bb86abec6_l3.svg" height="21" width="291" class="ql-img-displayed-equation " alt="\[ ax^n\cdot (bx^m+cx^p)=abx^{n+m}+acx^{n+p}\]" title="Rendered by QuickLaTeX.com"/> For example, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-6789509d82c2ec20c9ec0042faa482f3_l3.svg" height="22" width="270" class="ql-img-displayed-equation " alt="\[ -5x^2\cdot (3x^7-2x^2)=-15x^{9}+10x^{4}\]" title="Rendered by QuickLaTeX.com"/> When <strong>multiplying a binomial with a binomial</strong>, we must multiply each term in the first binomial with each term in the second binomial and add the resulting terms together. Specifically, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-2703bb64004068e8c07d02d1a9d98a0a_l3.svg" height="21" width="491" class="ql-img-displayed-equation " alt="\[ (ax^n+bx^m)(cx^p+dx^r)=acx^{n+p}+adx^{n+r}+bcx^{m+p}+bdx^{m+r}\]" title="Rendered by QuickLaTeX.com"/> For example, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-7c869780e9fd0eb9f86c7458010b620b_l3.svg" height="22" width="360" class="ql-img-displayed-equation " alt="\[ (x^9-2x)(6+4x^{-5})=6x^{9}+4x^{4}-12x-8x^{-4}\]" title="Rendered by QuickLaTeX.com"/> These rules easily extend to terms with multiple variables and to multiplying polynomials with polynomials. For example, confirm that you can justify each step of the following calculation: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-074dc67e292b6a8702620d9aa5e2f18f_l3.svg" height="78" width="3301" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-ebfc885aa5fcf724278a1e7f61e1ce87_l3.svg" height="78" width="549" class="ql-img-displayed-equation " alt="\begin{align*} -2(x^9-2xy+3)&(6y^2+4x^{-5})\\ &=-2\left(6x^{9}y^2+4x^{4}-12xy^3-8x^{-4}y+18y^2+12x^{-5}\right)\\ &=-12x^{9}y^2-8x^{4}+24xy^3+16x^{-4}y-36y^2-24x^{-5} \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> Alternatively, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-ddf4475af0a7fefe8c338228e8a9076b_l3.svg" height="78" width="3284" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-d6be96965b81b3fe76048b89d5287c64_l3.svg" height="78" width="540" class="ql-img-displayed-equation " alt="\begin{align*} -2(x^9-2xy+3)&(6y^2+4x^{-5})\\ &=(-2x^9+4xy-6)(6y^2+4x^{-5})\\ &=-12x^{9}y^2-8x^{4}+24xy^3+16x^{-4}y-36y^2-24x^{-5} \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> Which was strategically the better approach and why? <h4>Things To Watch Out For</h4> The negative sign causes no end of grief for a lot of people when working with multiplication. First, if a coefficient is not written explicitly, it is assumed to be 1. For example, look at

latex 2(4a + 6b) − (2a − 3b). This is the same aslatex 2(4a + 6b) + (−1)(2a − 3b). When you multiply a negative through an expression in brackets, all signs in the brackets will change. Continuing with the second term in the above example,latex −(2a − 3b)becomeslatex −2a + 3b. The expression then looks likelatex 2(4a + 6b) − 2a + 3b

    . In business, you will come across such problems often. For example, suppose that the revenue from sales of <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-3b90a1a1f76fb65ef1b602ffc7a867e0_l3.svg" class="ql-img-inline-formula " alt="x" title="Rendered by QuickLaTeX.com" height="8" width="10" style="vertical-align: 0px;"/> units of a product can be represented by <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-f500a4e428e31af154f2d252a1c538d5_l3.svg" class="ql-img-inline-formula " alt="R=-0.05x^2+20x" title="Rendered by QuickLaTeX.com" height="17" width="150" style="vertical-align: -2px;"/> and that the cost of producing <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-3b90a1a1f76fb65ef1b602ffc7a867e0_l3.svg" class="ql-img-inline-formula " alt="x" title="Rendered by QuickLaTeX.com" height="8" width="10" style="vertical-align: 0px;"/> units of the product is <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-3ed9746678241e3652c94371d76fd98a_l3.svg" class="ql-img-inline-formula " alt="C=1.2x+540" title="Rendered by QuickLaTeX.com" height="15" width="119" style="vertical-align: -2px;"/>. If you want to determine what the profit <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-d893ab70596b7ffecca5929c16176337_l3.svg" class="ql-img-inline-formula " alt="P" title="Rendered by QuickLaTeX.com" height="12" width="14" style="vertical-align: 0px;"/> is from the sale of <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-3b90a1a1f76fb65ef1b602ffc7a867e0_l3.svg" class="ql-img-inline-formula " alt="x" title="Rendered by QuickLaTeX.com" height="8" width="10" style="vertical-align: 0px;"/> units, i.e., revenue minus cost, you can calculate it as follows: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-b6adbc53a93533517b26f094c979efec_l3.svg" height="48" width="3318" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-235e6a696b49f779ec90cbb9c2c1b52f_l3.svg" height="47" width="578" class="ql-img-displayed-equation " alt="\begin{align*} P&=R-C=-0.05x^2+20x-(1.2x+540)=-0.05x^2+20x-1.2x-540\\ &=-0.05x^2+18.8x-540 \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> Note that we combined <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-2a9d2c68535abd64362bd19faf377be5_l3.svg" class="ql-img-inline-formula " alt="20x" title="Rendered by QuickLaTeX.com" height="12" width="28" style="vertical-align: 0px;"/> and <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-11a084b7b5a67c95053748606b85d83f_l3.svg" class="ql-img-inline-formula " alt="-1.2x" title="Rendered by QuickLaTeX.com" height="12" width="46" style="vertical-align: 0px;"/> above to get <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-073a29d373bc4b4b58942bf44ff28d1d_l3.svg" class="ql-img-inline-formula " alt="18.8x" title="Rendered by QuickLaTeX.com" height="12" width="41" style="vertical-align: 0px;"/> but all other terms stayed the same. This is because of the rules applied to adding and subtracting algebraic expressions with like terms. <div class="textbox textbox--examples"><header class="textbox__header"> Example: Simplifying Algebraic Expressions </header> <div class="textbox__content"> Simplify the following expressions: a. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-2cfa481516a3c0996ec7e26736946b6c_l3.svg" class="ql-img-inline-formula " alt="(6x+2+2)(3x-2)" title="Rendered by QuickLaTeX.com" height="19" width="155" style="vertical-align: -5px;"/> b. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-459cbf3c410e6e16336e4a757977a176_l3.svg" class="ql-img-inline-formula " alt="-(3ab)(a^2 + 4b - 2a) - 4(3a + 6)" title="Rendered by QuickLaTeX.com" height="20" width="254" style="vertical-align: -5px;"/> <strong>Answer</strong>: a. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-e0d30a6e2e3bbde00ee6cc61b726c7a4_l3.svg" height="71" width="3094" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-daa0ddc1615c5923d991b98f8816e638_l3.svg" height="71" width="345" class="ql-img-displayed-equation " alt="\begin{align*} (6x+2+2)(3x-2)&=(6x+4)(3x-2)\\ &=18x^2+12x-12x-8\\ &=18x^2-8 \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> b. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-dd23171831fa69a763b0bddd99750d11_l3.svg" height="48" width="3282" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-b83230e070982af4889606e838608521_l3.svg" height="47" width="533" class="ql-img-displayed-equation " alt="\begin{align*} -(3ab)(a^2 + 4b - 2a) - 4(3a + 6)&=(-3ab)(a^2 + 4b - 2a)-12a-24\\ &=-3a^3b-12ab^2+6a^2b-12a-24 \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> </div> </div> <h3>Division by a monomial</h3> You are often required to divide a monomial into either a monomial or another polynomial. When the denominator is not a monomial, it is either impossible or extremely difficult to simplify the expression algebraically. We will discuss here only the division where denominators are monomials, as in: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-f002eabe3a46bbbf739447dcc3ef8cd6_l3.svg" height="36" width="90" class="ql-img-displayed-equation " alt="\[\frac{polynomial}{monomial}\]" title="Rendered by QuickLaTeX.com"/> <div class="textbox shaded"> <h4>Dividing a polynomial by a monomial</h4> To simplify an expression when its numerator is a polynomial and its denominator is a monomial, apply these rules: <strong>Step 1:</strong> Simplify the numerator and the denominator as much as possible. For example, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-fb781b81d7b6b36b4781978281519343_l3.svg" height="39" width="348" class="ql-img-displayed-equation " alt="\[\frac{{3ab+3ab-3a^2b+9a{b^2}}}{{3ab}}=\frac{{6ab-3a^2b+9a{b^2}}}{{3ab}}\]" title="Rendered by QuickLaTeX.com"/> <strong>Step 2:</strong> Split the fraction into sum/difference of fractions for each term in the numerator and then simplify each term through division of monomials. For example, <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-84c74233be2e97e16085a400335d163f_l3.svg" height="109" width="3168" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-e6d9a272b53ed5767247e013a4ad6164_l3.svg" height="109" width="408" class="ql-img-displayed-equation " alt="\begin{align*} \frac{6ab-3a^2b+9ab^2}{3ab}&=\frac{6ab}{3ab}-\frac{3a^2b}{3ab}+\frac{9ab^2}{3ab}\\ &=\frac{6}{3}\cdot\frac{a}{a}\cdot\frac{b}{b}-\frac{3}{3}\cdot\frac{a^2}{a}\cdot\frac{b}{b}+\frac{9}{3}\cdot\frac{a}{a}\cdot\frac{b^2}{b}\\ &=2-a+3b \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> Note that this is equivalent to taking every term in the numerator and dividing it by the monomial in the denominator. <strong>Step 3:</strong> Perform any final simplification by adding or subtracting the like terms as needed. In the example above, as there are no more like terms, the final expression remains

latex 2 − a + 3b. You may have heard of an outcome called "cancelling each other out." For example, in resolving the divisionlatex \frac{{4a}}{{4a}}many people would say that the terms cancel each other out. Many people will also mistakenly interpret this to mean that the quotient is zero and say thatlatex \frac{{4a}}{{4a}} = 0<span style="color: #ff0000;">(wrong!)</span>. In fact, when terms cancel each other out <strong>in division</strong>, the quotient is one, not zero. The numerical coefficient islatex \frac{4}{4} = 1. The literal coefficient islatex \frac{a}{a} = 1Thus, latex \frac{{4a}}{{4a}} = \left( 1 \right)\left( 1 \right) = 1. This also explains why the definition of the zero exponent makes sense:latex \frac{{{a^1}}}{{{a^1}}} = {a^{1 – 1}} = {a^0} = 1

    . </div> <div class="textbox textbox--examples"><header class="textbox__header"> Example: Division by monomials </header> <div class="textbox__content"> Simplify the following algebraic expressions: a. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-1b79edd5dfeafd70ce0fd2909f651dc0_l3.svg" class="ql-img-inline-formula " alt="\dfrac{30?^6+5?^3+10?^3}{5x}" title="Rendered by QuickLaTeX.com" height="39" width="136" style="vertical-align: -12px;"/> b. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-c46595fc564a94c2796d87a718efe077_l3.svg" class="ql-img-inline-formula " alt="\dfrac{15?^2?^3+25??^2−?y+10?^4?+5??^2}{5xy}" title="Rendered by QuickLaTeX.com" height="43" width="251" style="vertical-align: -16px;"/> <strong>Answers:</strong> a. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-21d165b23eb8e54483962e8c9d8b915d_l3.svg" class="ql-img-inline-formula " alt="\dfrac{30?^6+5?^3+10?^3}{5x}=\dfrac{30?^6+15?^3}{5x}=\dfrac{30?^6}{5x}+\frac{15?^3}{5x}{5x}=6x^5+3x^2" title="Rendered by QuickLaTeX.com" height="39" width="485" style="vertical-align: -12px;"/> b. <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-bcd523720549dd1745f79289ad3ddaf9_l3.svg" height="134" width="3057" class="ql-img-displayed-equation " alt="\[ <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-198efda887cb9636bc5d2e51254412de_l3.svg" height="134" width="301" class="ql-img-displayed-equation " alt="\begin{align*} &\frac{15?^2?^3+25??^2−?y+10?^4?+5??^2}{5xy}\\ &=\frac{15?^2?^3}{5xy}+\frac{25??^2}{5xy}−\frac{xy}{5xy}+\frac{10?^4?}{5xy}+\frac{5??^2}{5xy}\\ &=3xy^2+5y-\frac{1}{5}+2x^3+y \end{align*}" title="Rendered by QuickLaTeX.com"/> \]" title="Rendered by QuickLaTeX.com"/> </div> </div> <h4><span style="font-size: 1em;">Paths To Success</span></h4> A lot of people dislike fractions and find them hard to work with. Remember that when you are simplifying any algebraic expression you can often transform a fraction into a decimal. For example, if your expression is <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-4faf1e68dd35551d3629ff008fb74338_l3.svg" class="ql-img-inline-formula " alt="\frac{{2x}}{5} + \frac{{3x}}{4}" title="Rendered by QuickLaTeX.com" height="22" width="55" style="vertical-align: -6px;"/>, you can convert the fraction into decimals: <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-1d6db508b42dc8c25aa08c77b0541b57_l3.svg" class="ql-img-inline-formula " alt="0.4x + 0.75x" title="Rendered by QuickLaTeX.com" height="15" width="96" style="vertical-align: -2px;"/>. However, if a fraction has non-terminating decimals (decimals go on and on), it is generally a bad idea to change the fraction to a decimal before the final calculation. This is because the decimal representation would only be an approximation of the actual value of the fraction and, as such, will likely introduce an error that can be compounded by other operations. This can result in a significant error in the final answer. <strong>If you must change a fraction to a decimal in a mid-step of your calculations, make sure that you round it to at least six decimals in order to minimize the risk of significant error in the final answer.</strong> <h3>Evaluation of Expressions Through Substitution</h3> The ultimate goal of algebra is to represent a relationship between various unknown quantities. Although it is beneficial to simplify these relationships where possible and shorten the algebraic expressions, in the end you often want to calculate a final value.<strong> Substitution</strong> involves replacing the variable components of an algebraic expression with known numerical values. Once the substitution has taken place, you calculate the value of the expression to determine the final value. <div class="textbox shaded"> <h4>How It Works</h4> Follow these steps to perform algebraic substitution when required to calculate a value of an expression: <strong>Step 1:</strong> Identify the task. For example, suppose the task is to evaluate <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-6dbe6c8257e247db399cafc032fae463_l3.svg" class="ql-img-inline-formula " alt="PV" title="Rendered by QuickLaTeX.com" height="12" width="28" style="vertical-align: 0px;"/>. <strong>Step 2:</strong> Identify a condition you know or are given that directly relates to the task. For example, suppose that you are given that <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-6dbe6c8257e247db399cafc032fae463_l3.svg" class="ql-img-inline-formula " alt="PV" title="Rendered by QuickLaTeX.com" height="12" width="28" style="vertical-align: 0px;"/> can be calculated using

latex {PV} = \frac{FV}{{1+rt}}. <strong>Step 3: </strong>Identify the values required for variables in the condition that describes the task. For example, suppose that you are given the valueslatex FV = $5,443.84,latex r = 0.12, andlatex t = \frac{270}{365}

    . <strong>Step 4:</strong> Take the known values and insert them into the equation that describes what you are looking for, and evaluate. In our example here, this results in <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-d3d47107f64063f72d3d8decb350e035_l3.svg" height="58" width="260" class="ql-img-displayed-equation " alt="\[PV = \frac{5443.84}{1+ 0.12 \cdot\dfrac{270}{365}}=\$ 5,000.00\]" title="Rendered by QuickLaTeX.com"/> </div> <h4>Things To Watch Out For</h4> It is common in algebra to represent a variable with more than just one letter. As you can see from the example above,

latex FVis a variable, and it represents future value. This should not be interpreted to be two variables,latex Fandlatex V. Similarly, PMT represents annuity payment. When you learn new formulas and variables, take careful note of how a variable is represented. As well, some variable names will contain subscripts. For example, you could see <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-058e93e03b156edb5ff47751c1540988_l3.svg" class="ql-img-inline-formula " alt="d_1" title="Rendered by QuickLaTeX.com" height="15" width="15" style="vertical-align: -3px;"/> and <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-ed2a0ccd170d35cc87a1d7381180a5a1_l3.svg" class="ql-img-inline-formula " alt="d_2" title="Rendered by QuickLaTeX.com" height="15" width="16" style="vertical-align: -3px;"/> in the same formula. What sometimes happens is that there is more than one value for the same variable. As you will learn in Chapter 6 about merchandising, when you buy an item you may receive more than one discount rate (what d stands for). Therefore, the first discount gets a subscript of 1, orlatex d_1, and the second discount gets a subscript of 2, orlatex d_2. This allows you to distinguish between the two values in the equation and substitute the correct value in the correct place. <h4>Paths To Success</h4> If you are unsure whether you have simplified an expression appropriately, remember that you can make up your own values for any literal coefficient and substitute those values into both the original and the simplified expressions. If you have obeyed all the rules and simplified appropriately, both expressions will produce the same answer. For example, assume you simplifiedlatex 2x + 5xintolatex 7x, but you are not sure if you are right. You decide to letlatex x = 2. Substituting intolatex 2x + 5x, you getlatex 2(2) + 5(2) = 14. Substituting into your simplified expression you getlatex 7(2) = 14. Since both expressions produced the same answer, you have direct confirmation that you have simplified correctly. <div class="textbox textbox--examples"><header class="textbox__header"> Example: Substitution </header> <div class="textbox__content"> Substitute the appropriate values to solve the following equation: <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-2df981473ab47a00cc8a24d0a951a99b_l3.svg" class="ql-img-inline-formula " alt="N = L(1 − d_1)(1 − d_2)(1 − d_3)" title="Rendered by QuickLaTeX.com" height="19" width="170" style="vertical-align: -5px;"/> where <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-77d008491fea956643939b7abfca65de_l3.svg" class="ql-img-inline-formula " alt="L = $1,999.99" title="Rendered by QuickLaTeX.com" height="16" width="95" style="vertical-align: -4px;"/>, <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-b6d8fe52c056c0ff1b7ac306d5b86198_l3.svg" class="ql-img-inline-formula " alt="d_1 = 35\%" title="Rendered by QuickLaTeX.com" height="17" width="73" style="vertical-align: -3px;"/>, <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-56e91d375132db1753da877559d64f86_l3.svg" class="ql-img-inline-formula " alt="d_2 = 15\%" title="Rendered by QuickLaTeX.com" height="17" width="73" style="vertical-align: -3px;"/> and <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-88384a5a446eb500448e0278afff8015_l3.svg" class="ql-img-inline-formula " alt="d_3 = 5\%" title="Rendered by QuickLaTeX.com" height="17" width="64" style="vertical-align: -3px;"/>. <strong>Answer:</strong> <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-5781d03d441421bdec8fc96485af5e1e_l3.svg" class="ql-img-inline-formula " alt="N = L(1 − d_1)(1 − d_2)(1 − d_3)=1999.99(1 − 0.35)(1 − 0.15)(1 − 0.05)=$1049.74" title="Rendered by QuickLaTeX.com" height="19" width="493" style="vertical-align: -5px;"/> </div> </div> <div class="textbox textbox--learning-objectives"><header class="textbox__header"> Exercises </header> <div class="textbox__content"> <h4>Mechanics</h4> For questions 1-4, simplify the algebraic expressions. 1.latex 2a − 3a + 4 + 6a − 32.latex 5b(4b + 2)3.latex \frac{{6{x^3}+12{x^2}+13.5x}}{{3x}}4.latex {(1 + i)^3} \cdot {(1 + i)^{14}}5. Evaluate the powerlatex {8^{\frac{2}{3}}}6. Substitute the known variables and solve for the unknown variable:latex I = Prtwherelatex P = $2,500, r = 0.06, and <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-df183836319f0be8b28ba15da841b0d1_l3.svg" class="ql-img-inline-formula " alt="t = \frac{135}{365}" title="Rendered by QuickLaTeX.com" height="22" width="53" style="vertical-align: -6px;"/> <h4>Applications</h4> For questions 7-11, simplify the algebraic expressions. 7.latex (6r^2+10-6r+4r^2-3)-(-12r-5r^2+2+3r)8.latex \left[ \dfrac{5x^9 + 3x^9}{2x} \right]^59.latex \dfrac{t}{2} + 0.75t – {t^3} + \dfrac{{5{t^4}}}{t} – \dfrac{{2\left( {t + {t^3}} \right)}}{4}10.latex \dfrac{14\left( 1+i \right)+21\left( 1+i\right)^4 – 35\left( 1+i\right)^7}{7\left(1+i \right)}11.latex \dfrac{R}{1+0.08\cdot \frac{183}{365}} + 3R\left( 1 + 0.08 \cdot\frac{52}{365} \right)12. Evaluate the power:latex \left[ \left( \dfrac{2}{5}\right)^2\right]^2For questions 13 and 14, substitute the known variables and solve for the unknown variable. 13.latex PV = \dfrac{FV}{\left( 1+i\right)^N}wherelatex FV = $3,417.24,latex i = 0.05, andlatex N = 614. <img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-d989c4b5dc6a71aab85af036373df765_l3.svg" class="ql-img-inline-formula " alt="PMT = \dfrac{FV}{\left[ \frac{\left( 1 + i \right)^N - 1}{i}\right]}" title="Rendered by QuickLaTeX.com" height="54" width="154" style="vertical-align: -30px;"/> wherelatex FV = $10,000, N = 17, andlatex i = 0.10. <h4>Challenge, Critical Thinking, & Other Applications</h4> For questions 15-17, simplify the algebraic expressions. 15.latex \left[\dfrac{10a^2b^3c^4}{5b^3c^4}\right]^2 + 6\left(a^8\right)^{1/2} – \left( 3a^2 + 6\right)\left(3a^2 – 3\right)16.latex \dfrac{- \left(5x+4y+3\right)\left(2x-5y\right)-\left(10x-2y\right)\left(2y+3\right)}{5}17.latex \dfrac{\left(-3z \right)^3}{\left(3z^2 \right)^2}{\left(2z^3\right)}^{ – 4}

    18. Substitute the known variables and solve for the unknown variable in: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-a5a8a345baef07b0c65912d2cd192421_l3.svg" height="97" width="380" class="ql-img-displayed-equation " alt="\[ FV_{ORD}=PMT(1+\Delta\%)^{N-1}\left[\frac{\left[\frac{\left(1+i\right)^{\frac{CY}{PY}}}{\left(1+\Delta\%\right)}\right]^N-1}{\frac{\left(1+i\right)^{\frac{CY}{PY}}}{\left(1+\Delta\%\right)}-1}\right] \]" title="Rendered by QuickLaTeX.com"/> where

latex PMT = $500,latex i = 0.05,latex Δ\% = 0.02,latex CY = 2,latex PY = 4, andlatex N = 20. For questions 19-20, evaluate the expression. 19.latex 50,000\cdot \left(1 + \dfrac{0.10}{12}\right)^{ – 27}20.latex 995\left[\dfrac{1-\left(1+0.02\right)^{13}\left(1+\frac{0.09}{4}\right)^{ – 13}}{\frac{0.09}{4}-0.02}\right]$

 

License

Icon for the Public Domain license

This work (Math Test by Morty Morterson and carl123) is free of known copyright restrictions.

Share This Book