4.4 2D Inequality and Absolute Value Graphs
Graphing a 2D Inequality
To graph an inequality, borrow the strategy used to draw a line graph in 2D. To do this, replace the inequality with an equal sign.
Example 4.4.1
Consider the following inequalities:
![\[\begin{array}{rrrrr} 3x&+&2y&<&12 \\ 3x&+&2y&\le &12 \\ 3x&+&2y&>&12 \\ 3x&+&2y&\ge &12 \end{array}\]](https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-ecfa38f2745dbab696d593195a9aba76_l3.svg "Rendered by QuickLaTeX.com")
All can be changed to 
by replacing the inequality sign with =.
It is then possible to create a data table using the new equation.
Create a data table of values for the equation 
 |
 |
|---|---|
| 0 | 6 |
| 2 | 3 |
| 4 | 0 |
| 6 | −3 |
Using these values, plot the data points on a graph.
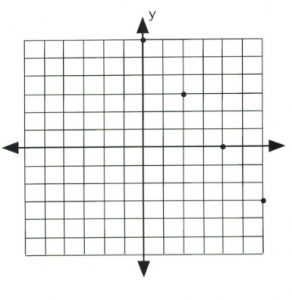
Once the data points are plotted, draw a line that connects them all. The type of line drawn depends on the original inequality that was replaced.
If the inequality had ≤ or ≥, then draw a solid line to represent data points that are on the line.
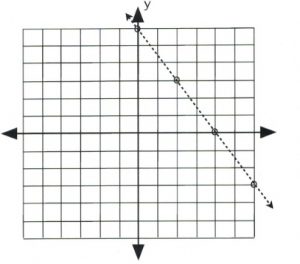
If the inequality had < or >, then draw a dashed line instead to indicate that some data points are excluded.
If the inequality is either 
or 
, then draw its graph using a solid line and solid dots.
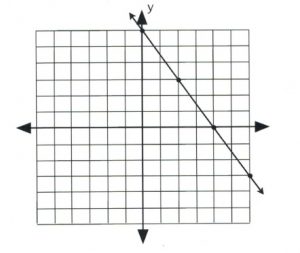
If the inequality is either 
or 
, then draw its graph using a dashed line and hollow dots.
There remains only one step to complete this graph: finding which side of the line makes the inequality true and shading it. The easiest way to do this is to choose the data point 
.
It is evident that, for 
and 
, the data point is true for the inequality. In this case, shade the side of the line that contains the data point .
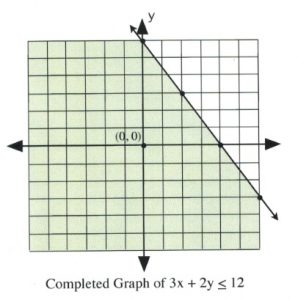
It is also clear that, for 
and 
, the data point is false for the inequality. In this case, shade the side of the line that does not contain the data point .
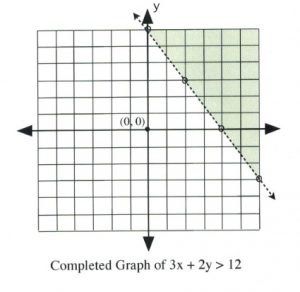12. The side without (0, 0) is shaded.” width=”300″ height=”292″>
Graphing an Absolute Value Function
To graph an absolute value function, first create a data table using the absolute value part of the equation.
The data point that is started with is the one that makes the absolute value equal to 0 (this is the -value of the vertex). Calculating the value of this point is quite simple.
For example, for 
, the value 
makes the absolute value equal to 0.
Examples of others are:
![\[\begin{array}{rrrrrrrrr} |x&+&2|&=&0&\text{when}&x&=&-2 \\ |x&-&11|&=&0&\text{when}&x&=&11 \\ |x&+&9|&=&0&\text{when}&x&=&-9 \\ \end{array}\]](https://integrations.pressbooks.network/app/uploads/quicklatex/quicklatex.com-afd21420d7f212edce3e17fed51a05e1_l3.svg "Rendered by QuickLaTeX.com")
The graph of an absolute value equation will be a V-shape that opens upward for any positive absolute function and opens downward for any negative absolute value function.
Example 4.4.2
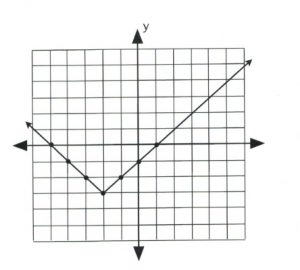
Plot the graph of 
The data point that gives the -value of the vertex is 
in which 
This is the first value.
For 
which yields 
Now pick -values that are larger and less than −2 to get three data points on both sides of the vertex, 
|
|
|---|---|
| 1 | 0 |
| 0 | −1 |
| −1 | −2 |
| −2 | −3 |
| −3 | −2 |
| −4 | −1 |
| −5 | 0 |
Once there are three data points on either side of the vertex, plot and connect them in a line. The graph is complete.
Example 4.4.3
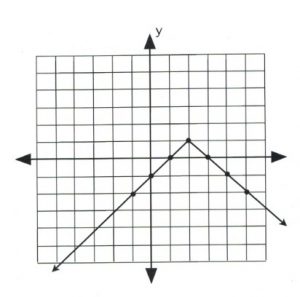
Plot the graph of 
The data point that gives the -value of the vertex is 
in which 
This is the first value.
For 
which yields 
Now pick -values that are larger and less than 2 to get three data points on both sides of the vertex, 
|
|
|---|---|
| 5 | −2 |
| 4 | −1 |
| 3 | 0 |
| 2 | 1 |
| 1 | 0 |
| 0 | −1 |
| −1 | −2 |
Once there are three data points on either side of the vertex, plot and connect them in a line. The graph is complete.
Questions
For questions 1 to 8, graph each linear inequality.
For questions 9 to 16, graph each absolute value equation.
