4.1 Solve and Graph Linear Inequalities
When given an equation, such as [latex]x = 4[/latex] or [latex]x = -5,[/latex] there are specific values for the variable. However, with inequalities, there is a range of values for the variable rather than a defined value. To write the inequality, use the following notation and symbols:
| Symbol | Meaning |
|---|---|
| > Greater than | |
| ≤ Greater than or equal to | |
| < Less than | |
| ≥ Less than or equal to |
Example 4.1.1
Given a variable [latex]x[/latex] such that [latex]x > 4[/latex], this means that [latex]x[/latex] can be as close to 4 as possible but always larger. For [latex]x > 4[/latex], [latex]x[/latex] can equal 5, 6, 7, 199. Even [latex]x =[/latex] 4.000000000000001 is true, since [latex]x[/latex] is larger than 4, so all of these are solutions to the inequality. The line graph of this inequality is shown below:

Written in interval notation, [latex]x > 4[/latex] is shown as [latex](4, \infty)[/latex].
Example 4.1.2
Likewise, if [latex]x < 3[/latex], then [latex]x[/latex] can be any value less than 3, such as 2, 1, −102, even 2.99999999999. The line graph of this inequality is shown below:
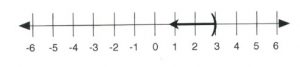
Written in interval notation, [latex]x < 3[/latex] is shown as [latex](-\infty, 3)[/latex].
Example 4.1.3
For greater than or equal (≥) and less than or equal (≤), the inequality starts at a defined number and then grows larger or smaller. For [latex]x \ge 4,[/latex] [latex]x[/latex] can equal 5, 6, 7, 199, or 4. The line graph of this inequality is shown below:

Written in interval notation, [latex]x \ge 4[/latex] is shown as [latex][4, \infty)[/latex].
Example 4.1.4
If [latex]x \le 3[/latex], then [latex]x[/latex] can be any value less than or equal to 3, such as 2, 1, −102, or 3. The line graph of this inequality is shown below:
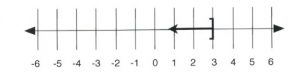
Written in interval notation, [latex]x \le 3[/latex] is shown as [latex](-\infty, 3].[/latex]
When solving inequalities, the direction of the inequality sign (called the sense) can flip over. The sense will flip under two conditions:
First, the sense flips when the inequality is divided or multiplied by a negative. For instance, in reducing [latex]-3x < 12[/latex], it is necessary to divide both sides by −3. This leaves [latex]x > -4.[/latex]
Second, the sense will flip over if the entire equation is flipped over. For instance, [latex]x > 2[/latex], when flipped over, would look like [latex]2 < x.[/latex] In both cases, the 2 must be shown to be smaller than the [latex]x[/latex], or the [latex]x[/latex] is always greater than 2, no matter which side each term is on.
For questions 13 to 38, draw a graph for each inequality and give its interval notation.
- [latex]\dfrac{x}{11}\ge 10[/latex]
- [latex]-2 \le \dfrac{n}{13}[/latex]
- [latex]2 + r < 3[/latex]
- [latex]\dfrac{m}{5} \le -\dfrac{6}{5}[/latex]
- [latex]8+\dfrac{n}{3}\ge 6[/latex]
- [latex]11 > 8+\dfrac{x}{2}[/latex]
- [latex]2 > \dfrac{(a-2)}{5}[/latex]
- [latex]\dfrac{(v-9)}{-4} \le 2[/latex]
- [latex]-47 \ge 8 -5x[/latex]
- [latex]\dfrac{(6+x)}{12} \le -1[/latex]
- [latex]-2(3+k) < -44[/latex]
- [latex]-7n-10 \ge 60[/latex]
- [latex]18 < -2(-8+p)[/latex]
- [latex]5 \ge \dfrac{x}{5} + 1[/latex]
- [latex]24 \ge -6(m - 6)[/latex]
- [latex]-8(n - 5) \ge 0[/latex]
- [latex]-r -5(r - 6) < -18[/latex]
- [latex]-60 \ge -4( -6x - 3)[/latex]
- [latex]24 + 4b < 4(1 + 6b)[/latex]
- [latex]-8(2 - 2n) \ge -16 + n[/latex]
- [latex]-5v - 5 < -5(4v + 1)[/latex]
- [latex]-36 + 6x > -8(x + 2) + 4x[/latex]
- [latex]4 + 2(a + 5) < -2( -a - 4)[/latex]
- [latex]3(n + 3) + 7(8 - 8n) < 5n + 5 + 2[/latex]
- [latex]-(k - 2) > -k - 20[/latex]
- [latex]-(4 - 5p) + 3 \ge -2(8 - 5p)[/latex]

